All the methods we have used to reach space so far have been subject to the Tsiolkovsky rocket equation - propellant must be ejected and more and more of it is needed to go further.
The tether
The simple description is that a rotating tether, consisting of a strong cable with an attachment point at the tip and an anchoring counterweight at the center, will be able to catch and throw payloads without requiring a rocket engine. The process of hooking onto a payload to accelerate it into a new trajectory will transfer momentum from the counterweight to the payload, causing the tether to slow down. In reverse, a payload can be caught and slowed down, transferring momentum back into the counterweight and speeding it up. The ability to transfer momentum back and forth is why these structures are also called momentum exchange tethers.
 |
| NASA has long studied this option. |
In this post, we will go into more detail on what is needed to create a functional rotating tether, how it can be used and what its potential effects are on space travel and industry could be.
The mechanics
 |
| Using a tether to move from one orbit to another, in this case LEO to GEO. |
The idea to use a long tether to climb into space without expelling propellant is an old idea. A huge tower extending up past the atmosphere was described by Tsiolkovsky. It is ironic that the person who first described how hard spaceflight by rocket is, due to the exponential nature of the deltaV equation, is also the person who described the best way to side-step that problem with non-rocket launch.
The material requirements for a full space elevator are extreme. The only practical way to build it would be to use carbon nanomaterials, but extended to a scale of multiple kilometres instead of the micrometres we struggle to produce consistently in a laboratory today. It is why we must turn to something that provides some of the same benefits without the same stringent requirements.
For this, there is the orbital tether concept.
A large object in orbit, such as a satellite, space station, captured asteroid or similar, can serve as an anchor point to extend a strong cable down to a lower altitude. A payload can grab onto the lower end of the cable and climb up to the altitude of the anchor point. This climb does not require the use of propellant.
The simplest design is a stationary orbiting elevator that provides a deltaV benefit based on the difference in orbital velocities at high and low altitudes.
 |
| An LEO to GEO elevator. |
In the example above, an space station orbits at 2,000 km altitude, at an orbital velocity of 6.89 km/s. It performs one orbit in about 2 hours and 7 minutes. The lower tip extends down to an altitude of 200 km. It retains its orbital period but the distance it travels is much less, so velocity is reduced to 5.41 km/s. A circular orbit here is 7.78 km/s, so it provides a 2.37 km/s saving. The upper tip reaches up to 3,860 km altitude. It covers much more distance with the same orbital period, so velocity increases to 8.43 km/s, compared to the 6.24 km/s of everything else orbiting at that altitude. It is a 2.19 km/s boost. In total, we get a 4.56 km/s benefit.
Huge altitude differences are needed to create the potential for significant deltaV savings. Because the lower tip of the tether is travelling at orbital velocity, it cannot extend too far down either; as it would encounter the atmosphere and burn up.
 |
| A tether boost facility designed to be launched from a DeltaIV. |
A rotating tether does away with those limitations. The velocity of its tips and the speeds at which it can capture or release payloads can vary greatly from the orbital velocity of the anchor point. It can be much shorter too.
At its lowest point, the tip of a rotating tether will be travelling at orbital velocity minus the rotation velocity. At its highest point, the two velocities will add up. The length of the tether itself will place the tips at very different altitudes at their highest and lowest points. Moving a payload between these altitudes is an additional benefit.
Let’s imagine a modestly-sized tether orbiting at a high altitude above the Earth. It is 1,000 km long, orbiting at 1,100 km altitude and rotating once every 70 minutes. Its lowest point is 100 km above the surface of the Earth. Its highest point extends to an altitude of 2,100 km. Tip velocity is 1.5 km/s. It is tapered from base to tip to minimize its mass.
 |
| Tapered tethers are the lightest design. |
Orbital velocity at 1,100 km is 7.3 km/s. At its lowest point, the tether tip will be travelling at 5.8 km/s relative to the ground. At its highest point, this value becomes 8.8 km/s.
If a suborbital craft launched from the ground to try to catch up with the tip at its lowest and slowest, it would need to expend a deltaV of about 6.8 km/s. It can then quickly transfer a payload onto the tether. The payload then starts its 35 minute journey up around to the opposite end of the tether. It experiences an average acceleration of 0.23 g while doing so.
At the top of the tether, it is released into a trajectory that forms an ellipse with its periapsis at 2,100 km altitude and its apoapsis at 13,500 km. It can then expend an additional 1.4 km/s of deltaV to reach the Moon, or about 1.6 km/s to escape the Earth entirely.
If a typical 350s Isp kerosene-oxygen rocket is used, then it needs a total deltaV of about 8.2 km/s to ride the tether to the Moon. Meaning, it has an overall mass ratio of 10.9. However, if there is no tether available, then the deltaV requirement rises to 12.5 km/s and the mass ratio required balloons to 38! The tether is effectively saving 4.3 km/s of deltaV and leading to a much smaller rocket.
The tether can also help with returning from the Moon. The spacecraft swoops down from lunar altitude (384,400 km) to a rendezvous with the tether at 2,100 km altitude. It would be travelling at 9.6 km/s, so it needs to spend an additional 0.8 km/s of deltaV to slow down enough to match the 8.8 km/s velocity of the tether's upper tip. In return, it avoids having to slam into the atmosphere and instead is swung down for much gentler aerobraking. The weight savings from having a thinner heatshield could more than make up for the propellant consumed, especially if this is a reusable vessel.
Note that tethers do not have a single velocity for catching and releasing payloads. It is in fact a range of velocities, from zero up to the tip velocity. For capture at lower velocities, a payload can aim to intercept the tether at a point closer to the base of the tether. Halfway up the tether means a redezvous at half the tip velocity. The same goes for release; not releasing from the tether tip means a lower velocity. You can imagine a vehicle launching up from the ground to catch the tether tip at its lowest point, and instead of swinging around to the other side, just slowly climbing up the tether until it can hop off from the anchor station. This puts it in an orbit parallel to the anchor station, which is great if you are not trying to fly off to the Moon or beyond.
However, making use of this flexibility means adding a way to prevent the unused length of the tether from striking the payloads coming in for a rendezvous, as well as providing structures that allow payloads to climb up and down the tether (although they can be as simple as a pulley and cables).
 |
| The ISS regularly is regularly reboosted against the effects of drag. |
And of course, none of these deltaV savings are for ‘free’. Accelerating payloads means the tether will slow down. If it slows down too much, it will de-orbit itself. The momentum lost with each catch-and-release operation must be recovered either by absorbing momentum from payloads being slowed down, or by using its own propulsion system.
A major advantage of an orbital tether is that you do not have to immediately recover that momentum - it gives time for slower but more efficient propulsion systems like a solar-electric thruster to gradually accelerate the tether. A chemical propulsion system limited to 450s of Isp is not needed as the acceleration can be done over time with something that has thousands of seconds of Isp. The propellant needed to run the tether’s engines is greatly reduced. Even more interesting is the possibility of propellantless propulsion, such as electrodynamic tethers that push off the magnetic fields around a planet.
 |
| Electrodynamic tether reboost. |
Another advantage is that the tether can ‘store’ excess momentum. It can accelerate itself to a more energetic orbit with a higher velocity. For example, a tether in a 2,000x2,000 km circular orbit could accelerate by 1 km/s to reach a 2,000x9,565 km orbit. It can still capture payloads at the same 2,000 km altitude, but it will have an additional 1 km/s of velocity to use. The extra velocity can be used to accelerate the same payloads faster, more numerous payloads to the same speeds or larger payloads than possible before.
Tether masses and velocities
 |
| Tether structure and materials for the early TSS-1 experiment in orbit. |
The tether materials determine how fast the tips can rotate. Each material has a certain characteristic velocity, given by:
- Characteristic velocity = (2 * Tensile Strength / Density)^0.5
Characteristic velocity is in metres per second.
Steel is strong, with a maximal strength of 2,160 MPa for AerMet 340, but dense, at 7,860 kg/m^3. This gives it a characteristic velocity of 741 m/s.
The aramid fiber Kevlar is stronger and lighter, managing 3,620 MPa with 1,440 kg/m^3. Its characteristic velocity is 2242 m/s.
The strongest material we can mass-produce today is Toray’s polyacrylonitrile fiber T1100G. It can resist 7,000 MPa while having a density of 1,790 kg/m^3, so its characteristic velocity is 2,796 m/s.
If we can describe the tip velocity as a multiple of the characteristic velocity, then we can use a much simpler equation to work out how much a tether will mass. We’ll call this the Velocity Ratio or VR.
For example, 1.5 km/s is a VR of 2.02 for steel but only a VR of 0.54 for T1100G.
The tether mass will be directly proportional to the payload mass. If it has to pull up a 1 ton payload, it will be ten times heavier than if it only needs to pull on 100 kg payloads. Using the VR, we can calculate the tether mass ratio using this equation:
- Tether Mass Ratio = 1.772 * VR * e^(VR^2)
Tether Mass Ratio is a multiple of the payload mass, in kg.
Using the previous example, a 1.5 km/s steel tether will have to be 211.8 times heavier than its payload. A T1100G tether would only be 1.28 times heavier than its payload. This is a significant difference. The e^(VR^2) portion of the tether mass equation highlights just how important it is to use strong yet lightweight materials and to keep the tip velocity close to the characteristic velocity.
Here is a graph showing how tether mass increases with the Velocity Ratio for different materials:
It should be noted that all of these calculations are for a tether with no safety margins. Any sort of variation, such as vibrations from the counterweight or an imperfect capture of the payload, would snap it. A minimal safety margin might be 50%. Crewed spacecraft might demand a 200% margin or more. What this means in practice is that the maximum payload the tether could handle is reduced to create a safety margin.
To overcome the limitations of the tether tip velocities, the tether can move into higher energy orbits. For example, a tether with a 1.5 km/s tip speed starts off in a circular 2000 km altitude orbit moves itself into a 2,000x1,000,000 km orbit. It can still capture payloads at the same altitude but it now does so at a velocity of 9,391 m/s instead of 6,897 m/s. This gives it 36% more momentum to give, and it can release payloads at a velocity of up to 10,891 m/s relative to the Earth. This is beyond the escape velocity at that altitude! If the tether had stuck to its initial 2000km circular orbit, its tip speed would have had to be 4 km/s instead, which would have meant an exponentially higher mass ratio.
As the tether collects and releases payloads, it must adjust the distribution of its mass to maintain its center of rotation.
 |
| Adjusting the tether with a moving counterweight on a 'crawler'. |
This can be done by shifting the counterweight, moving additional masses up and down the tether, changing the length of the tether using motors and/or having a dynamic suspension system that also helps dampen vibrations.
In later sections, we will go through the various ways tethers can be used and combined to cover the entire Solar System.
Skyhook
| The skyhook process from Hoyt. |
Getting off Earth and into orbit is a massive task. It requires that over 9 km/s of deltaV be delivered in one chunk, by a high thrust propulsion system. Chemical rockets can do this, but they end up as balloons of fuel with a small payload on the tip.
A skyhook can help reduce deltaV requirements where they are hardest to deliver: at the end of a tiresome fight against Earth’s gravity. Because of the exponential nature of the Tsiolkovsky rocket equation, the last 1 km/s of deltaV costs much more than the first 1 km/s. The savings enabled by a Skyhook are therefore disproportionately high.
Imagine a 200 km long tether anchored to a station orbiting at 400 km altitude. Its tip speed is 2.4 km/s. This means it travels over the ground at 5.3 km/s at its lowest point, and swings above at 10.1 km/s.
A rocket trying to catch up with this tether at its lowest point must deliver 5.3 km/s of horizontal velocity, but also about 1.5 km/s to reach a 200 km altitude as well as make up for drag and gravity losses on the way up. Its deltaV requirement becomes 6.8 km/s. With kerosene and oxygen propellants delivering an average Isp of 330s, it would need a mass ratio of 8.17. This is well within the reach of a single-stage vehicle, even with margins to return and land vertically for reuse.
For comparison, a kerosene/oxygen-fuelled vehicle that must make orbit would need 9.5 km/s and a mass ratio of 18.8. It would need multiple stages and it would be difficult to create deltaV margins for recovery. The tether-assisted rocket is 2.76 times smaller and lighter for the same payload!
But that’s not all.
The tether swings around and launches its payload into a 400 x 35,800 km orbit. This is also known as a geostationary transfer orbit (GTO) - an orbit where a rocket would only need an extra 1.5 km/s to turn into a 35,800 x 35,800 km geostationary orbit.
The tether’s top-side boost is worth another 2.4 km/s. If it has to be delivered by the same vehicle that must reach orbit on its own, deltaV requirements would add up to 11.9 km/s. With 330s Isp propulsion, this means a staggering mass ratio of 39.5. Modern rockets get around this by fitting their upper stages with more efficient rocket engines, but they still take a huge hit to their payload capabilities when launching to GTO instead of LEO. ULA’s Delta IV Heavy could launch 28 tons into LEO but only 14 tons into GTO.
We could do better. A faster tether that dips deeper into the atmosphere is possible, further reducing the deltaV requirements for meeting it and reducing the constraints on the vehicle we use.
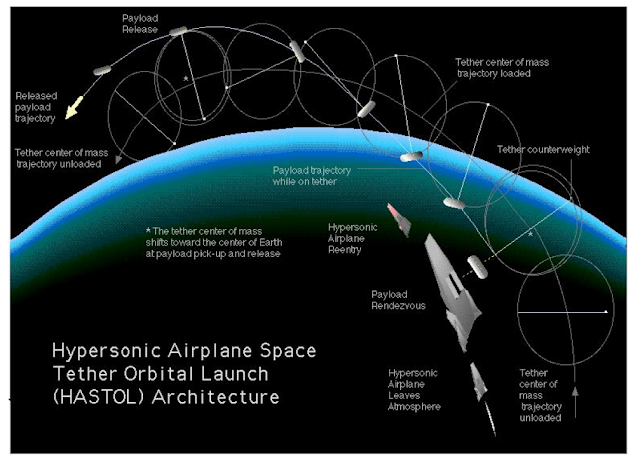 |
| HASTOL. We don't really want the plane to exit the atmosphere. |
1.7 km/s corresponds to Mach 5 at this altitude. We have had aircraft reach these speeds and altitudes for decades, under rocket power. We have developed hypersonic scramjets that can sustain these speeds much more efficiently too. A large aircraft could meet a Hypertether using existing technologies reliably, without needing a lot of propellant or excessive thermal shielding. The exponential mass ratios that make rockets so expensive no longer come into play. Hypersonic rendezvous vehicles could climb to this altitude using engines with Isp exceeding 4000s (using hydrogen fuel), fly long enough to attempt multiple rendezvous with the tether (one attempt per tether rotation period) and land, ready to fly again within the hour.
The downside to this approach is that the mass ratio of the tether itself becomes unwieldy. At 6 km/s, even T1100G tethers require a mass ratio of 379. The result is huge tethers in orbit needed to handle even the smallest of payloads. With a 200% safety margin, a 1 ton payload would need a 758 ton tether in these conditions. Launching such a mass into space and fitting it with an appropriately sized counterweight and anchor point would require hundreds of launches to break-even with the cost.
A staged tether can get around some of these difficulties.
Just like a rocket, a tether can be broken up into stages. Each stage uses the tip of the previous tether as its anchor point. If two 3 km/s tethers are staged, then they could achieve a combined 6 km/s tip velocity. However, each stage only needs a mass ratio of 6, with T1100G. A 1 ton payload would need 1x6: 6 ton first stage tether and a (1+6)x6 : 42 ton second stage tether. Add a 200% safety margin and it would still be an overall mass of 84 tons, which is much lower than the previous 758 tons for a single tether.
Many difficulties must be overcome with this design. The first is the need to absorb any lateral movement which could cause tether sections to run into each other. The second is to create a stable joint that can operate under huge stresses. Using some of the mass savings from a staged tether design to alleviate these problems is recommended. Finally, each tether stage will be relatively short, leading to high centrifugal forces being imposed. If a 200 km long tether is divided into two 100 km sections, each rotating at 3 km/s, then payloads would be subjected to an acceleration varying between 9 and 18g. Much longer tethers would be needed for human travellers.
Overcoming these difficulties would yield a flexible Hypertether with exceptional performance but low mass.
 |
| A huge, slowly rotating skyhook would not look much different from a section of space elevator near the ground. |
The ideal skyhook, as originally conceived for science fiction, uses multiple stages so that its combined tether tip velocity matches its orbital velocity. It would become stationary relative to the ground with each rotation. This means a combined 7.7 km/s for a tether orbiting at 250 km altitude. No rendezvous vehicle is needed; payloads would simply sit on the ground and latch onto the descending hook from the sky.
A huge number of additional challenges face this ‘perfect Skyhook’ design, ranging from the need to prevent unpredictable air turbulence from smashing tether stages into each other, to needing thermal protection for tethers that accelerate to multiple km/s while coming up through the thickest portions of the atmosphere.
High performance skyhooks around Earth will mostly aim to lift payloads up from the ground and out into space. They are likely to run at a permanent momentum deficit; propulsion is essential. Obtaining propellant is an obstacle, as are the power requirements.
The simplest solution is to sacrifice a portion of each payload using the tether to carry propellant. Low performance tethers that sit at high altitudes and with low tip velocities will make this a very expensive option. This is because they make rendezvous vehicles work hard to get to them. If a 1,000 ton tether station accelerated a 3 ton payload by 3 km/s from rendezvous to release, it would lose 9 m/s itself. Accelerating 1000 tons by 9 m/s using a 3,000s Isp engine requires about 305 kg of propellant. This means that, roughly, for every 9 payloads accelerated by the tether, a 10th launch is needed for refuelling. High performance tethers have it worse. They lose more momentum proportionally with each payload they accept, because of their higher tip speeds. Accelerating a 3 ton payload by 12 km/s slows down a 1,000 ton tether by 36 m/s, requiring 1,223 kg of propellant to recover! Thankfully, they make travel to space so much cheaper that sacrificing every third payload for propellant still makes for an overall saving over rockets.
Extraterrestrial sources of propellant can be much more interesting. It normally takes less deltaV to move propellant from the Moon to LEO than it takes to move it up from the ground to LEO, at about 5.8 km/s vs 9.5 km/s. With aerobraking, the deltaV required to return from the Moon’s surface to Earth orbit is reduced to 2.8 km/s. Lunar sources of propellant remain interesting even when we adjust the deltaV requirements to account for the tether helping out. A tether with 3.1 km/s tip velocity would reduce the deltaV needed to lift off from Earth’s surface and enter into Low Earth Orbit to 6.4 km/s. It would also reduce the deltaV needed for a spaceship to launch off the Moon and enter Low Earth Orbit to 2.8 km/s. This keeps lunar sources of propellant the better option over terrestrial sources.
Another advantage of extraterrestrial propellants for tethers is that capturing them ‘recharges’ the momentum of the tether. Catching 1 ton of propellant coming in at 3 km/s would accelerate a 1,000 ton tether by 3 m/s. Using that propellant for a 3,000s Isp thruster would further accelerate it by 29 m/s. That propellant is worth 10% more than expected!
The absolute best propellant source of Skyhooks around Earth is the atmosphere itself. Atmospheric gas scooping is discussed in full detail here. A tether tip dipping into the atmosphere can ‘cheat’ the gas scooping retention equation by collecting gases at a lower velocity than the tether station’s orbital velocity. For example, a tether at 250 km altitude rotating at 3 km/s would collect gases at a velocity of 4.7 km/s. If a 3000s Isp engine running on nitrogen and oxygen is used, up to 84% of gases collected can be retained. The gases retained can then be fed to rockets using the tether, turning it into an orbital fuel depot.
What’s more exciting is that it removes the restriction from the tether to have high Isp engines in the first place. They are bulky and power-hungry equipment. A tether that only aims to regain velocity would be satisfied with 0% gas retention. Lighter, simpler propulsion options like nuclear thermal rockets, with an Isp of just 480s, become acceptable. Alternatively, we could use hydrogen-oxygen chemical rocket where payloads coming up the tether provide 12% of the propellant and the remaining 88% is oxygen collected from the atmosphere.
Better than any propellant source is not having to use any propellant. This is important for very high altitude tethers that do not meet the atmosphere. Electrodynamic propulsion pushes off the magnetic field around Earth. It only consumes electricity. Although the thrust per kW is very low, it is a reliable and already tested option.
Powering all these propulsion options is another concern. Ideally, a tether station would want a compact and long-duration power source like a nuclear reactor. Solar panels are also available, but they require hefty energy storage solutions from the periods where the tether is in the Earth’s shadow, and the drag from the exposed panels adds to the momentum loss over time. Between these two options is the possibility for beamed power. Whether it is from the ground or a space station far above, energy can be transmitted over microwaves or a laser beam to the tether station, where it is converted back to electricity with high efficiency.
 |
| From Hop David's excellent blog. |
Such a Moonhook would only need a tip velocity of about 1.5 km/s when orbiting at a 400 km altitude.
Because of the lower velocities involved, it can be very lightweight, and easy to transport into a lunar orbit from Earth. There would be no erosion from passing through gases, and it would only have to avoid lunar mountains (up to 6km high) when coming down.
This tether can help transfer payloads to the lunar surface, but also to other interesting locations, such as the L1 or L2 Lagrange points. It could be the centerpiece of a cislunar economy, and unlike the ‘lunar elevator’ concept, it does have to extend across hundreds of thousands of km to be useful.
 |
| Phobos elevator suggested here. |
Reasons for a moonhook also apply to other moons. Phobos is a popular destination for small moonhooks, enabling access to the martian surface for 2.14 km/s.
It could relay work with a tether around Deimos to enable a zero-propellant transfer into and out of the martian system.
Interplanetary trajectories
As mentioned in the previous section, tethers can easily fling payloads far beyond Earth.
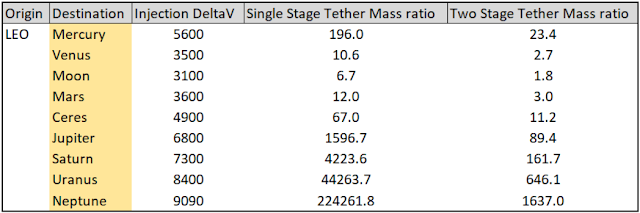
Here is a table of tether tip velocities needed to place payloads on Hohmann transfer trajectories to different planets:
Injection DeltaV is the velocity increase in meters per second that the payload must receive to enter a trajectory that takes it near the destination. Another propulsion system is needed to actually slow down once it arrives.
The mass ratio calculations are done for T1100G cables. You will notice that some destinations, like Mars or Venus, are well within the capabilities of reasonably sized tethers. Mercury or Ceres can be reached with very heavy tethers. Going beyond Jupiter strictly necessitates the use of staged tethers, with Neptune probably off-limits for an Earth-based tether.
The DeltaV values listed above are for Hohmann trajectories. For the Outer Planets, minor increases in deltaV (8400 m/s instead of 8200 m/s for Uranus, for example) were selected to enable missions that took less than 10 years to perform. Tethers can speed up travel between planets, by entering payloads into higher energy trajectories.
Here is another table showing how much travel times (in days) can be reduced by tethers with 4, 6 and 8 km/s tip velocities.
Venus and Mars are the greatest beneficiaries of an extra boost from a faster tether. Mars sees up to 5 times shorter trips when using an 8 km/s tip velocity tether. When the injection deltaV becomes more demanding, the benefit is reduced.
A good idea is to have spacecraft using tethers employ their own propulsion system. They can act as an additional ‘stage’ with their own mass ratio between propellant and payload. As we calculated before, staging massively reduces the difficulty of reaching a certain velocity.
Here is an example:
A spaceship using 450s Isp chemical rockets loads up 2 kg of fuel for each 1 kg of dry mass. This gives it a mass ratio of 3 and a total deltaV of 4850 m/s. It performs a rendezvous with a 6 km/s two-stage tether made out of T1100G cables. The first tether stage has a mass ratio of 12, to get a tip velocity of 3000 m/s and a 100% safety margin on top. The second tether stage also has a mass ratio of 12.
The final mass ratio of this system is 3 x 12 x 12: 432. The final velocity of 10,850 m/s enables trips to Jupiter in as little as 325 days, or to Uranus in 1551 days. A two-stage tether that tries to achieve this velocity would have had a mass ratio of over 22,000, while a single stage tether would have needed a ridiculous 23.8 megatons of cables for each ton of spaceship.
Working through calculations like these really helps highlight just how similar a tether stage and its characteristic velocity is to a rocket stage and its exhaust velocity.
Tether trains and interplanetary networks
A tether can hand over a payload to another tether.
These tethers can be in different orbits, and have different tip velocities, so long as the relative velocity falls to zero during a rendezvous. Three interesting scenarios for tether handovers can be considered:
-Exchange between circular orbits
A tether in a low orbit can fling a payload up to an altitude that intersects with a tether in a higher orbit. It is caught and further boosted from this higher orbit. Or, payloads can be sent down from the higher tether.
Here is an illustrated example:
It can work best when the higher tether is a geostationary space station, or these tethers are transporting payloads between different moons around a gas giant like Jupiter. The most interesting aspect is that the tethers can keep each other from losing momentum, so long as the masses they exchange are balanced. The lower tether is naturally larger, as it has to send payloads up with a greater velocity. It could set up a ‘train’ of many momentum-neutral exchanges with several tethers.
-Exchange with eccentric orbits
In this exchange, one of the tethers is in a low circular orbit and the second tether is in an eccentric orbit with the lowest point (the periapsis) intersecting the first tether’s orbit.
Here is an illustrated example:
The main advantage is that the tether’s own velocity is added to the boost it can provide a payload. Multiple tethers can be used in sequence, bridging the velocity gap between a tether in a low circular orbit and a very eccentric, near-escape orbit. Low Jupiter Orbit at 42 km/s and Jupiter Escape Velocity at 60 km/s are separated by an 18 km/s gap. Three tethers with tip velocities of 4.5 km/s can relay a payload between them. It does not have to be done all within the narrow window where tethers are all lined up at the lowest point of their respective trajectories. The transfer between orbits can be done one by one.
The tether in the lowest orbit accelerates a payload at 4.5 km/s. It is received by a second tether with a tip velocity of 4.5 km/s. The combined boost is 9 km/s. This is done again, to reach a third tether station that is on a near-escape trajectory, with a periapsis velocity of just under 60 km/s. Any extra boost from this third tether would allow a payload to escape into interplanetary space. A full 4.5 km/s boost can put it on a trajectory that sends it all the way back to Earth.
Using tethers like this will put the deep gravity well of Jupiter on the same level of accessibility as Mars or Venus. The energy-intensive transfer of crew or cargo up and out of Jupiter can be compensated for by slowing down equal masses of ‘junk’ such as iceball comets or discarded asteroids.
We can also expand the use of ‘tether trains’ to interplanetary space. Stations orbiting the Sun on circular or eccentric orbits could pass payloads between them for ‘free’, so long as momentum exchanges are balanced.
 |
| A tether attached to a small body, as envisioned here. |
These tethers can be anchored to asteroids, moons or mobile bases, much like the slow Aldrin Cycler concepts. Payloads can hop between tethers at these points gaining or losing velocity.
 |
| A cycler station makes a trip between Earth and Mars on a regular orbit. |
Cyclers are most interesting as they perform orbits that take many years, but with tethers, they can send payloads between them much faster.
Moving between cyclers in this manner can take on aspects of a train stopping between towns, especially if the cyclers gain large enough populations to become noteworthy destinations on their own. This can lead to a ‘Wild West’ aesthetic, or fulfil the need to visit new locations without having to cross interplanetary distances.
A Solar System tethered together
A switch in transport of payloads from expensive, slow, propellant-consuming rockets to rapid, low to zero-propellant tethers would have an outsized effect on human expansion into the Solar System.
Human passengers will see great reductions in travel times. The combination of an initial boost from a tether, with deltaV provided by a spaceship’s propulsion system, will connect the Inner planets within a matter of weeks. Tethers provide the option to collect propellant more easily, which means those spaceships can afford to spend a lot more propellant than they otherwise could, in turn making travel even faster. Even the Outer planets could be reachable within a few months of travel time. That’s a great step up from multiple years. Enough perhaps to prevent distant colonies from becoming the destination for a ‘once-in-a-generation migration’.
Cheaper, quicker travel for humans means that automation is not needed as much. Machinery doesn’t have to work for years on end without maintenance, as a repair crew could arrive regularly. A more mobile population means that space becomes open to less skilled, less experienced workers to fill in job positions wherever they appear, instead of every station or outpost having to rely on multi-skilled workers that can handle prolonged isolation. More people moving around means better chances that ‘extras’ like luxuries and personal services can be accommodated, improving living conditions and so on, in a positive feedback loop.
Inert cargo will also benefit from tether transportation. High value goods can be exchanged quickly. A latest generation computer processor wouldn’t have to spend years being exposed to cosmic rays before it reaches a colony around Jupiter as an out-of-date and damaged product. Profits can be made on platinum ground metals a few weeks after they are mined; this means adventurous asteroid mining companies don’t have to hold onto cash reserves so that they can operate for months in between deliveries. They can be smaller, leaner and take more risks.
On the other hand, larger payloads can be moved at the same speed with tethers for much less cost. An exchange between two tethers, one on Mars and one on Earth, can take the regular minimal-energy Hohmann trajectory. However, far less propellant would be needed (if any at all, with momentum-neutral exchanges). The payloads would not need any engines, heatshields or large cryogenic propellant tanks. With the use of tugs to maneuver the payloads into a rendezvous at either end, they won’t even need expensive guidance systems. Such cheap travel opens up many new possibilities. Asteroid mining usually considers elements like iron and aluminium to be ‘wastes’ as their value is too low to be worth moving around. Their only use would be at the site they are extracted from. This no longer has to be the case; a much larger fraction of an asteroid becomes exploitable. A beneficial side-effect is that accessing these low-value resources to build up a colony in a remote corner of the Solar System becomes even more affordable.
 |
| Complete this scene with a spinning tether in the background. |
Large, slow payloads that can easily be outrun by tether-boosted spacecraft opens the door to piracy. A better transportation system helps with the methods discussed in these previous posts. A ‘pirate tether’ can fling spacecraft into intercepts with payloads in transit. Criminal ports would have higher performance tethers to catch diverted goods from odd angles and high velocities. This is especially useful for stealth craft that can use a tether to boost into a trajectory without announcing themselves, and don’t want to reveal the location of their safe haven by slowing down using rockets.
Anything criminals can do, the military can do better. Tether boosts means warships are closer to targets than before. Reduced reliance on onboard propulsion for deltaV means that more mass can be dedicated to armor and weapons instead of propellant tanks. Also, as mentioned before, a secret network of tethers can be employed to move stealth craft around the Solar System. Munitions launched like this can be smaller and easier to hide too.
Further developments
Everything mentioned so far is only the start of what is possible with tethers.
 |
| The use of tethers as aerodynamic devices is under-explored. |
Their use and performance can be expanded over time, as new ideas appear or better technologies are matured.
We could consider a hybrid of a stationary and rotating tether. A rotating hub could be installed at the lower end of a very long stationary tether. It would collect a payload and transfer it to another rotating tether at the upper end by climbing up a stationary segment. The main advantage of this hybrid tether is that it can greatly extend the use of small, low velocity rotating tethers, while also not having to fully cover the distance to the destination like a simple stationary tether would have to.
Supermaterials can also be considered. Tethers don’t need carbon nanotubes to function, but they can make great use of them. The characteristic velocity of graphene (130 GPa strength, 2267 kg/m^3) is 10,709 m/s. A tether to payload mass ratio of 10 enables a tip velocity of 12.3 km/s. A staged tether can get this up to 24.3 km/s with a total mass ratio of 100. That’s enough to fling a payload out of Low Jupiter Orbit with one single tether, or enable trajectories from Earth to Mars in 34 days, or to Saturn in 360 days. Between two tethers, we could see velocity gains of over 50 km/s… the main limitation would become human endurance. Even with a 6g tolerance limit, a tether tip velocity of 24.3 km/s means a minimum tether length of 10,000 km to reduce centrifugal forces!
Going further, tether transport networks can be tied into the Inter-Orbital Kinetic Energy Exchange networks for transporting and generating energy, described here. Tethers can set up the exchange of masses, or even convert them into electricity themselves by using an electrodynamic tether in reverse: instead of consuming electricity to push against a magnetic field, using the field to generate a current while braking against it.
Finally note that we haven’t considered the Oberth effect and that tethers can exploit it. Sending a payload down into a gravity well before rapidly accelerating it gives it an extra boost that does not match the momentum lost by the tether. The faster the tether tip, the greater the effect.














One small error: Where you meant to put the table of tether tip velocities for Hohmann transfers, you put the graph of tether mass ratio vs tether tip velocity again.
ReplyDeleteAnd you are definitely right about short tethers not being good for manned spacecraft, due to the large acceleration - and multi-stage tethers probably aren't either unless they are *very* large, due to the quickly changing centrifugal acceleration.
I've done some math on it, and for a single stage tether in Earth Orbit with the tip dipping to 50 km altitude at 1.5 km/s earth-relative velocity (to allow easy access by scramjet vehicles), if it is to be limited to 3 g acceleration, you'd need a tether length of ~1180 km, a tip velocity of ~5800 m/s, and the thing rotating about three times per hour. But of course the benefit is that that would give you 13 km/s tip velocity relative to earth at the top of the swing.
If you want to limit acceleration to 1 g, the tether length grows to a bit over 2700 km, but tip velocity decreases slightly to 5120 m/s.
Of course, neither is that feasible without nanomaterials - with T1100G, you have, with no margins, a mass ratio of 250 for the first, and of 90 for the second.
Though this shows off very neatly the high dependence of mass ratio on velocity ratio - an almost threefold increase in mass ratio for less than a 15% increase in tip velocity.
And of course, with nanomaterials it becomes more than feasible. Graphene's characteristic velocity allows for a mass ratio of 10, at a factor of safety of over 6 - something more characteristic of structural civil engineering rather than aerospace engineering.
DeleteThanks for pointing out that mistake! It's been fixed now.
DeleteThe strange thing about their tethers is that their mass does not depend on their length. A shorter tether that has to handle the same loads as a longer tether will mass the same. However, shorter tethers are easier to control and they are less vulnerable to being hit by debris and micrometeorites.
I would always recommend splitting a boost between multiple tethers to reduce g-loads and get an overall lower mass ratio (6 km/s from two tethers instead of one tether, for example), but lifting off Earth is a special case.
I know that you discussed the use of atmospheric scoops in combination with mid-high isp rockets on tethers designed to drop down into the atmosphere, but how feasible would that be for a low mass ratio tether? I guess the question I'm really trying to ask if how heavy a given tether would have to be, not to be strong enough to lift cargo, but in order to retain enough velocity to regenerate it's momentum. If a given tether only has a mass ratio of 10, would lifting a piece of cargo not significantly effect its orbital trajectory?
ReplyDeleteHi Spencer.
DeleteYou don't need to collect a large amount of propellant all at once to feed a high Isp engine. You can choose to carry only, let's say, 1 kg every cycle. A 50km long tether with a tip velocity of 3km/s would perform about one rotation every 105 seconds, giving you an average mass flow of 9.5 g/s.
This is enough for a 4.1 MW, 3000s Isp engine to overcome the drag of a massive 100,000m^2 installation in Low Earth Orbit (200km altitude).
This tether would need a relatively high mass ratio, but it is multiplying a very small mass to begin with, so the tether become manageable.
Do you intend to cover the tether catapult systems?
ReplyDeleteI'm not sure what you mean by 'tether catapult' systems, but I will be expanding on this topic.
DeleteApologies! Should have been more precise...
Deletehttps://en.wikipedia.org/wiki/Momentum_exchange_tether#Tether_cable_catapult_system
In summary: "A tether cable catapult system is a system where two or more long conducting tethers are held rigidly in a straight line, attached to a heavy mass. Power is applied to the tethers and is picked up by a vehicle that has linear magnet motors on it, which it uses to push itself along the length of the cable. Near the end of the cable the vehicle releases a payload and slows and stops itself and the payload carries on at very high velocity."
Basically a combination of tether and mass driver.
I'll look into it.
DeleteI am not sure of the math involved, but, I wonder whether you could take advantage of either the earth's magnetic field or atmospheric differences in charge at different heights to help power such devices.. just thinking of how spiders use static electricity to hurl themselves even across oceans... https://www.pbs.org/newshour/science/spiders-fly-on-the-currents-of-earths-electric-field
ReplyDeleteYes, you can!
DeleteElectrodynamic tethers can push against the Earth's magnetic field to either accelerate (while consuming electricity) or slow down (while generating electricity).
Using atmospheric drag is less interesting as it can only slow you down.
Is it possible too weaponize tethers? maybe as a way too sustain slinging projectiles at enemies?
ReplyDeleteTethers do not make for good weapons. They are too slow, cannot really be aimed, are very predictable and very are vulnerable to damage.
DeleteHowever, they can help with getting missiles and spacecraft into fighting positions more easily.
Do torch drives have a place in a tether dominate sol system? Seeing as a tether system can deliver the shortened travel times most torch drive concepts offer.
ReplyDeleteTorch drives would make travel so fast and cheap that tethers would not compete with them over interplanetary distances.
DeleteHowever, their ability to move things quickly in between orbits around a planet, or between nearby moons, would still be useful as you would not have to activate a dangerous and radioactive drive in those locations. Also, tethers would still be useful for their military ability to deploy stealth ships and weapons.
I knew I had seen this before, and it finally hit me, this is an update of Hans Moravec's work, which I read about in one of Jerry Pournelle's books, I believe. "Staging" of tethers is a new wrinkle, and the idea fits nicely into my speculation that bulk cargos will be simply sent around in unpowered "pods" to reduce expense. Using a tether rather than a mass driver certainly makes it much simpler and cheaper (always important), but the high velocities still leaves the issue of these pods becoming weapons by accident ot on purpose due to the huge kinetic energy they carry.
ReplyDeleteFor those interested in the original work, the link is here: https://frc.ri.cmu.edu/~hpm/project.archive/1976.skyhook/papers/endsky.pox
I'll go an read that.
DeleteSpace tethers are a really old idea, I'm just putting together different variants and expansions on what people have already come up with decades ago.
Matter Beam, is it appropriate/is there any point to commenting on older posts at this point?
DeleteThank You,
No, please continue. I welcome it.
DeleteThank you for this article! There are two novels that came out in 1979 in which space tethers figure prominently: Charles Sheffield's The Web Between the Worlds and Arthur C. Clarke's The Fountains of Paradise. These novels are credited with popularizing the idea of space elevators. I enjoyed both of them.
ReplyDeleteI have a question WRT to ED tethers: the magnetosphere wobbles and bends as it gets buffeted by the solar wind. Does this mean that an ED tether would produce different amounts of thrust on sun-facing or sun-blocked sides of the planet? Or that it might not produce any thrust at all during a solar storm (as the magnetosphere gets compressed)?
ReplyDeleteAlso a nitpick: T1100G is a carbon fibre. PAN is merely used as a precursor in fabrication.
DeleteThat's an interesting complication. I haven't found that issue cited in any of the papers I've read about electrodynamic propulsion, perhaps because the effect is small in LEO, deep inside the magnetosphere. It would definitely be a factor to consider for tethers that extend beyond the LEO though... but then again, space weather is a good thing for scifi!
DeleteLate answer.
ReplyDeleteThanks for the great blog post and your collaboration video with kurzgesagt, which was a really good intro to Skyhooks and Space Tethers.
I also found this video showing a nonrotating Skyhook, which really intrigued me since it looked like an evolved version of our current Space Station, which let me wonder how near in the future the concept might be.
https://vimeo.com/175424301
In a discussion a while ago, somebody dismissed the concept as too dangerous and complicated and that just giving rockets bigger fuel tanks would be easier. What would be your counterargument?
Hi Vineyard. Thanks for that, I appreciate it.
DeleteWe have physically tested tethers in space, so this propulsion concept is as real as nuclear rockets and megawatt ion thrusters.
They are not more dangerous than other objects in space. You simply have to clear a larger volume to avoid the chance of a collision.
Making rockets bigger is not really a good solution, as they give exponentially diminishing returns, and the cost increases massively for small increases in deltaV. The 'easier' argument makes more sense if you consider avoiding the deployment of a new technology at a large scale a worthwhile objective. As space transportation grows in volume, the tether will look more and more reasonable as a cost-saving and extra performance measure.
Wow, thx for the fast answer.
ReplyDelete"You simply have to clear a larger volume to avoid the chance of a collision."
Imo. this really has to be done big time. kurzgesagt has also made a real good video about how Space Junk could really mess up our future in Space. (and a german blogger lately also said that the current trend with LEO satellite constellations is sadly accelerating that trend.)
How much instantaneous acceleration does the payload experience on hooking-on to the bottom of the tether?
ReplyDeleteIt will be similar to the centrifugal acceleration experienced at the tip of the tether. For large tethers that don't have to rotate quickly, it can be very mild acceleration (1-2 gees).
DeleteWhat about an asteroid fly-by rotorvator bola. A nickle iron is cable cut in half like Kursk. One lobe dropped-the tail hooked to a huge payload-and that gets yanked up and the other paylobe drops down?
ReplyDeleteI have trouble imagining how this works from this description. Do you have a link or a document I can read about it?
DeleteMay be we can design a kind of static(not rotating ) tether above earth ,Venus,Mars.The main part of the tether is a photovoltaic space staion,it's between the lowest part and highest part of the tether,and provides electrity for ion engines and elevators.Only these bodies are suitable.That's because these bodies have atmosphere,on the lowest part of tether,we can install
ReplyDeleteair collecters to absorb airs and inject them to maintain the trajectory.we can also use these gas to produce goods.A plate for ssto to landing and transport.
An elevator can be used to make goods ascend to the main part of the tether.
I've calculated,it can reduce the dv to Leo for about 3000m/s,a ssto with 6500m/s dv is possible.And the highest part of the tether can throw the spacecraft to moon.
ffff
ReplyDeleteIt occurs to me that in a Tillotsen or rotating two-stage tether, the second (outer) stage would not rotate at a constant speed. Because of the acceleration due to first-stage motion (or gravity, in the Tillotsen case), the second stage would move slower on the inside part of its swing. So if you were trying to use a two arms on the second stage 180 degrees out of phase to counterbalance each other, it wouldn't work: they would not always be in a straight line. (unless maybe in a very short and fat tether, the second stage had enough bending stiffness to overcome this effect and force the two second stage arms to rotate like one piece at constant speed). The resulting, variable component of force would be applied to the tip of the first stage. I haven't really thought about whether this would be a problem. Maybe it would require the first stage to be significantly stronger. Maybe it would cause chaotic double-pendulum effects.
ReplyDeleteWhere does the 2 come from in the characteristic velocity equation? Other versions I have seen of this equation the maximum velocity is just the square root of the tensile strength/density.
ReplyDelete