The rocket equation is often described as tyrannical. Low exhaust velocity chemical rockets that are used today need payloads to be mounted on towers of propellant to reach extraterrestrial destinations.
Re-fueling a rocket in orbit has been floated as a solution to drastically reduce rocket sizes. The best source of propellant for this purpose is much closer than is generally thought...
Orbital refuelling |
| Orbital propellant depot |
The propellant can be launched separately or manufactured from extra-terrestrial sources such as the Moon or an asteroid. In this post, we will be looking at a way to simply scoop up propellant from the atmosphere.
Beating the rocket equation
A quick calculation reveals how advantageous orbital refuelling is.
 |
| SpaceX's Mars mission architecture relies on orbital refueling for good reason. |
The rocket equation is as follows:
- DeltaV = Exhaust velocity * ln(Mass Ratio)
We can re-write that equation to work out the mass ratio required to obtain a certain deltaV.
- Mass ratio = e^(DeltaV/Exhaust Velocity)
This means that the wet mass is 15.9 times greater than the dry mass on the launchpad.
Going from orbit to Mars requires a mass ratio equal to e^(5600/3433): 5.1
 |
| DeltaV requirements for travel between Earth, Moon and Mars. |
What if we use orbital refuelling?
 |
| How reusability and orbital refueling can make a Moon mission drastically smaller |
The mass ratio on the ground is therefore 15.9. The rocket will mass only 159 tons on the launchpad. This is a rocket more than five times smaller than the previous example.
Using the same calculations with the Moon as destination (3300m/s) still means the rocket is e^(3300/3343): 2.61 times smaller than without refuelling.
Current challenges and solutions
 |
| ITS and its tanker docking in LEO to transfer propellants. |
 |
| Building a lunar base. |
However, it would require a massive investment in extraterrestrial infrastructure that would not help anyone for several decades, requiring automated technology that can work independently or a permanent manned settlement.
 |
| China Aerospace Science and Technology Corp.'s 30km/s Hall-effect ion thruster. |
 |
| Dawn approaching Ceres. |
High Isp rockets could reduce the mass ratio required for a mission to mars down to e^(5600/30411):1.2 or less. It would be more than four times smaller than a chemically-fuelled rocket.
Atmospheric Gas Scooping
This concept consists simply of running a gas scoop through the upper atmosphere and collecting the atmospheric gasses to be used as propellant. Some of the propellant is consumed by the scoop itself, the rest of made available for orbital refuelling of other craft.
 |
| The PROFAC gas scoop operated at 120km altitude and was powered by a 10MW reactor (4) and had some rocket fuel on-board to burn with collected oxygen to produce thrust in case the reactor failed. |
The momentum a scoop loses by collecting 1 kilogram of air at low altitude is 1*7800: 7800 Newton-seconds of momentum. The momentum gained by using a rocket is equal to exhaust velocity*propellant flow. The exhaust velocity*propellant flow product must be greater than 7800 Newton-seconds.
If the exhaust velocity is lower than orbital velocity, the scoop will need to consume more propellant than it could ever collect to stay in space.
If the exhaust velocity is equal to orbital velocity, the scoop has to use all of the gasses it collects as propellant and retains none. This is the case for solid-core nuclear thermal rockets.
If the exhaust velocity is higher than orbital velocity, then the scoop will be able to retain some of the gasses in reserve and produce a net gain in propellant collected.
The ratio between propellant retained and propellant consumed is simple. A rocket like Dawn's ion engine will produce 1*30411: 30411 Newton-seconds of momentum per kilogram of propellant. It can therefore retain up to (30411-7800)/30411: 0.743 or 74.3% of the gasses it collects.
The gas retention percentage is simply calculated as:
- Retention % = [(Exhaust Velocity - Orbital Velocity)/Exhaust Velocity]* 100
Powering the scoops against drag
Running an electric rocket requires a good amount of power. In space, this is hard to come by.
The power requirements of a gas scoop are determined by the thrust it needs to produce, which depends in turn on the drag it experiences. Aerodynamics play no role at orbital velocities, drag is only a function of cross-section and atmospheric density. This equation will give you an estimate within +/-10% of reality.
- Drag: 0.5 * Orbital velocity^2 * Cross-section area * Gas density
Orbital velocity will be in m/s.
 |
| Gas density chart up to 300km altitude from here. |
Gas density is determined by altitude and noted in kg/m^3. If the scoop operates at a single altitude, we use a single value. If it changes altitude, we use an average value based on the time spent at each altitude. At very high altitudes, some sources will note a value in particles per cubic meter. This has to be converted into kg/m^3.
 |
| Particle counts for different elements per cubic meter for altitudes up to 1000km. |
So how much power do we need?
We first must estimate the drag generated and give the scoop ship enough power to produce sufficient thrust to counter the drag, plus a safety margin.
 |
| The ISS reboosts its orbit using a Zvezda module's engines. It could be performed by electric rockets instead. |
We can see that above 200km altitude, the drag force is in millinewtons, descending down to tenths of micronewtons per square meter at the edge of the atmosphere. A more accurate reading would take into account the small differences in orbital velocity as the altitude changes. It is 7800m/s at 150km altitude, but reduces slightly to 7350m/s at 1000km altitude.
The equation for engine power is the following:
- Engine Power: Thrust * Exhaust Velocity /2
- Engine Power: Drag force per m^2 * Cross-section * Exhaust Velocity /2
Example:
10m wide funnel at 200km
Cross-section area: (10/2)^2 * 3.14 = 78.5m^2
Drag force per m^2 at 200km: 9.51 * 10^-3 Newtons
Exhaust velocity: 30411m/s
Engine power: 11.35kW
100m wide funnel at 400km
Cross-section area: (100/2)^2 * 3.14 = 7850m^2
Drag force per m^2 at 400km: 1.03 * 10^-4 Newtons
Exhaust velocity: 30411m/s
Engine power: 12.3kW
The engine power here is the effective power output going out of the nozzle. Rocket engines are not 100% efficient, and there are further losses in the systems that generate, transport and convert electricity going into the engine. These might double the actual power consumption.
There are many options for producing the required energy to power the engines, but only a few are practical or achievable with the technologies available in the near future.
 |
| Apollo's fuel cells. |
The two options remaining are solar panels and nuclear reactors.
Solar panels are cheap and lightweight, able to produce over 580W/m^2 at peak efficiency. However, they can become very large if we need kilowatts of power. They must be packed behind the main funnel or they would increase the cross-section area. A 10kW array of solar panels might be divided into eight segments 2m wide and 1.07m long. Thin-film solar panels might reduce mass down to a few dozen kilograms.
Nuclear reactors are very powerful and are unlikely to need much mass or volume to produce the output required. Experiments have been conducted and prototypes have been flown of space-rated nuclear reactors, but historical and political reasons have prevented their widespread use. We can send a 100kW reactor today into space massing only 512kg.
Gas collection and processing
 |
| A turbomolecular pump |
The first step is to move the pressurized gas into an empty gas tank. It can be vented without any pumping equipment and only a valve to maintain the flow going one way. As long as the collection tanks are kept at a lower pressure, no active pumping is needed.
To keep collection tanks at a lower pressure, the gasses must be cooled until they become liquid, then they are transferred to an insulated long-term storage tank. This is the second step.
 |
| Air intake and compression are tasks performed by the scoop during its operation. |
 |
| Number of N2 particles per cubic centimeter at altitudes 100 to 1000km |
 |
| Number of O2 particles per cubic centimeter at altitudes 100 to 1000km |
 |
| Number of atomic nitrogen N particles per cubic centimeter at altitudes 100 to 1000km |
 |
| Number of atomic oxygen O particles per cubic centimeter at altitudes 100 to 1000km |
 |
| Number of atomic hydrogen H particles per cubic centimeter at altitudes 100 to 1000km |
For example, at 200km altitude, we note that we get 3.8*10^9 N2 particles, 3.25*10^8 O2 particles, 4.39*10^9 O particles, 9.62*10^6 N particles and 2.15*10^5 H particles per cubic centimetre. We multiply the values by a million to get the cubic meter values, then convert the particle numbers into masses by multiplying by the element's molar mass in g/mol then dividing by Avogadros' constant (6.022 * 10^23).
We can work out the following figures:
N2 particle mass: 28.0134 / 6.022 * 10^23 = 4.65 * 10^-23 grams
N2 mass per m^3 at 200km: 1.78 * 10^-16 kgO2 particle mass: 31.9988 / 6.022 * 10^23 = 5.313 * 10^-23 grams
O2 mass per m^3 at 200km: 1.72 * 10^-17 kg
O particle mass: 15.9994 / 6.022 * 10^23 = 2.65 * 10^-23 grams
O mass per m^3 at 200km: 1.16 * 10^-16 kg
N particle mass: 14.0067 / 6.022 * 10^23 = 2.325 * 10^-23 grams
N mass per m^3 at 200km: 2.23 * 10^-19 kg
H particle mass: 1.008 / 6.022 * 10^23 = 1.67 * 10^-24 grams
H mass per m^3 at 200km: 3.59 * 10^-21 kg
What can we understand from these figures?
The atmospheric composition at 200km is dominated by nitrogen and monoatomic oxygen. Density when all gasses are considered is 3.127*10^-16kg/m^3... nitrogen therefore represents 56.9% of the mass of air collected at this altitude, with monoatomic oxygen second at 37%. The relative proportions of the gasses allows us to estimate the average heat capacity; it should be about 1.2kJ/kg/K.
 |
| Stirling engine animation |
Here is a table of the temperatures, energies and power consumption levels involved in liquefying air collected at 7800m/s for altitudes between 100 and 1000km:
Note that the power ratings are in milliWatts per square meter of scoop cross-section area. It is the electrical consumption for a heat pump cooling down the gasses from the collection temperature to 77K, where nitrogen liquefies.
For 200km, we read that 19.48W per square meter is required. A 10m wide scoop would need to devote only 1.5kW to cryocooling at this altitude.
Gas scoop design example
We will attempt to work out a ballpark estimate of the mass, size and performance of a conventional gas scoop that uses currently available technology.
This simple design operates at one altitude and continuously uses its engines counter the drag forces of ramming through the air.
We will stay within the limits of a payload that could be launched by a single Falcon 9 FT rocket to LEO, so 22.8 tons to 200km altitude.
Let's start with the engine. We want it to use the gasses it collects as propellant. This excludes current electric rockets propelled by xenon or argon. Instead, we need to find examples of designs that are happy to run on nitrogen. Oxygen is viciously corrosive when hot, so should be avoided as a propellant despite its relative abundance.
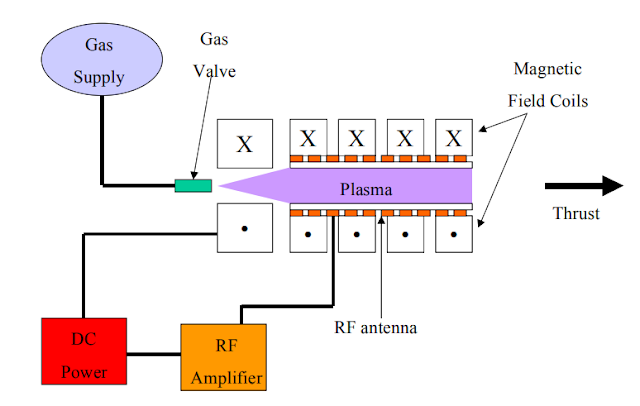 |
| Diagram of the electrodeless RF plasma thruster. |
 |
| The VASIMR rocket engine by AdAstra. |
As mentioned before, solar electric power is the most realistic option. Supplying 1kW of electricity using thin-film technology requires 2.02m^2 of solar panels and about a kilogram of electrical equipment after including 15% losses during electrical conversion and transport to the engines.
Putting all these figures together gives us a figure of 34kg and 2.02m^2 of power and propulsion per Newton of thrust.
At 200km altitude, the orbital velocity is 7790m/s. Air density is 3.127*10^-10 kg/m^3. The drag force per square meter of scoop cross-section area is 9.487*10^-3 N/m^2.
Using the power and propulsion figures, we determine that each square meter of scoop area requires roughly 0.326kg of equipment to counter drag forces.
A drag force in the range of milliNewtons allows for the use of very lightweight scoop materials. The closest analogy would be a hemispherical balloon holding up to a pressure differential, with structural support lines transmitting load or tension forces to a payload. Stratospheric balloons survive 200Pa pressure differentials and carry several tons using membranes massing 55 grams per square meter.
We might be able to say that despite the hundred-thousand-fold decrease the in the forces involved we have decided to include massive redundancies against micrometeorite impacts and friction ablation so the scoop will mass 0.05kg/m^2, similar to a stratospheric balloon.
Processing the gasses requires some more equipment. 2.44 micrograms per square meter per second. are collected at this altitude and velocity. 94% of that is N2 and O, reducing the collected mass to 2.29 * 10^-9 kg/m^2/s. It requires a heat pump and gas handling system able to handle 18W of power. SABRE reaction engines claims to be able to handle 400MW of cooling with a one ton device, but we will use a much more conservative 400W/kg. 18W of cooling would require 0.045kg of equipment.
The total so far is 0.426kg/m^2.
We want our gas scoop to collect gasses for one year, then offload them. We therefore need storage tanks able to handle liquid oxygen and nitrogen for one year. They store at similar temperatures, so we will use 5% of the propellant mass as tank mass, something based on this NASA report for the Jupiter launch vehicle. It is based on Aluminium-Lithium materials, but even more lightweight carbon fibre is possible.
 |
| World's largest carbon-fibre tank for holding liquid oxygen. |
Due to the 23000 to 7800 ratio between the engine's exhaust velocity and orbital velocity, 33.9% of the gasses collected must be expelled as propellant. This will reduce the amount of nitrogen collected from 56.9% to 22.98% of the total mass of gasses collected. This reduces the nitrogen storage volume required by a factor 2.47 and the yearly tank mass to 4.67 * 10^-5 m^3, and the mass to 2.3 grams.
With all functions accounted for, the scoop will require 0.428kg of equipment per m^2 of cross section area. If we double this figure to account for everything including attitude thrusters, docking structures, thrust frames, communications, propellant handling, safety margins and so on, it is still about 0.857kg/m^2.
Now we can derive the maximum size of this scoop and its yearly performance.
22800kg / 0.857kg = 26604m^2
A single Falcon 9 FT can put a scoop with a cross-section area of 26604m^2 into orbit. It would represent a disk 184 meters wide, although multiple smaller scoops would be more sensible. They would be equipped with thrusters producing a total 252 newtons of thrust and use 509m^2 of solar panels.
These scoops would collect 2046 tons of gas, of which 471 tons of liquid nitrogen and 757 tons of liquid oxygen is retained, for a total of 1228 tons.
What's the point of all this?
Remember the mass ratio equations at the beginning of this post? A mass ratio of 15.9 to reach orbit can be understood as each kilogram of propellant in orbit being worth 15.9 times more than the same kilogram on the ground.
1128 tons in orbit would be worth 19525 tons on the ground. These thousands of tons could be saved without having to capture an asteroid, mine the moon or invent a radically new launch system. They alone would make the entire concept of atmospheric gas collection worthwhile.
Understandably, the gasses collected cannot be simply loaded into rocket propellant tanks and expected to burn. Liquid nitrogen is inert and cannot be 'burned'. Liquid oxygen needs a fuel, which can be liquid oxygen, methane or kerosene lifted up from the ground or already on-board the spaceship expecting to be refuelled.
In a typical LH2/LOX rocket engine, six kilograms of oxygen are consumed for every kilogram of hydrogen. Looking at it another way, for each kilogram of liquid oxygen a spaceship receives through orbital refuelling, it needs to carry along 0.167kg of liquid hydrogen from the ground or separate launches.
A 10 ton dry mass spaceship being sent from low earth orbit to geostationary orbit would require a deltaV of 3931m/s. If it uses a LH2/LOX 450s Isp rocket engine, it would require 14.3 tons of propellant. It would need to bring up 2.39 tons of liquid hydrogen from the ground, but would save on 11.96 tons of liquid oxygen propellant.
The lifter on the launchpad would be 49% lighter.
A single Falcon 9 FT-launched scoop could provide enough liquid oxygen to push 633 tons of payload from LEO to geostationary orbit per year.
For comparison, a 353s Isp kerosene/liquid oxygen rocket with an oxidizer/fuel ratio of 2.56 would reduce lifter mass on the launchpad by 52% and is enough for 498 tons to GEO.
There are further savings if we consider that that launcher would need smaller propellant tanks, structures and fewer engines when it is nearly two times smaller. LEO to GEO is a common requirement for satellite launches. These savings might allow for much more realizable Lunar or Martian missions.
Other secondary benefits exist.
The name 'Orbital Transfer Vehicle' or OTV is given to the rocket stage that moves a payload from low earth orbit to geostationary or lunar orbits. EDS stands for 'Earth Departure Stage' for payloads being sent to Mars or elsewhere. An electric or nuclear-thermal OTV or EDS can use all of the gasses collected (1228 tons) and can essentially launch with empty tanks, meaning that the full advantages of orbital refuelling can be reaped.
The availability of hundreds to thousands of tons of propellant waiting in orbit will incentivise the development of non-chemical propulsion technologies.
Alternative designs and improvements
The two heaviest components of an atmospheric scoop are power and propulsion equipment.
Here are some solutions to reducing their mass requirements so that even bigger scoops which can collect even more gas per year can be launched on the same launcher:
-Use all the nitrogen:
If atmospheric gas scooping is going to provide oxidizer to spaceships in low orbit, then only liquid oxygen is of interest. All the liquid nitrogen can be converted into propellant on-board the scoop. At 200km, this allows for up to 57% of the gasses collected to be consumed, meaning Isp can be as low as 18km/s and thrust per kg will increase by a third compared to our example.
Furthermore, if the nitrogen is being consumed as it is collected, then there is no need to liquefy it and less cryocooling equipment will be needed.
-Use better power density and space-grade components:
In our example, the power density of the electric rocket engine was 580W/kg, cryocoolers were 400W/kg and we doubled the mass per square meter in the end. Specialized technology using space-grade materials could greatly reduce the mass per square meter.
-Trawler design
 |
| Instead of fish, it would be collecting gasses from a lower altitude. |
If the main body of the design and its scoop funnel were physically separated, the overall design could be lighter. An arrangement where the funnel is dragged at a lower altitude by tethers and pumps connecting it to the main body is called a 'trawler', as it resembles boats dragging along nets under the sea. For one, solar panels can be arranged any way desired. Second, a scoop traversing lower altitude air can collect more gas per square meter, allowing for a smaller cross-section for the same performance and lower mass per square meter. Third, the scoop ship does not have to consume a lot of propellant to lift itself out of a lower altitude if it wants to stop scooping: it can simply winch up the funnel.
The disadvantages are greater complexity and the need to pump gasses from where they are collected to where they are processed and stored.
-Diver design
A conventional or trawler gas scoop design needs engines to counter-act drag with an equal amount of thrust at all times. Solar panels must provide sufficient energy and store it to keep propulsion running around the night side of Earth.
There is a design that allows a scoop ship to get away with much smaller engines and power sources. A 'diver' operates at an elliptical orbit, dipping into the atmosphere only at its lowest point. At that point, it rapidly scoops up gas and rams its way up and out with its momentum. For the rest of the orbit, it fires up its small engine to recover the lost momentum over a long period of time. Much smaller solar panels would be needed to feed propulsion and gas processing equipment. If the diver goes into the lower atmosphere with excess velocity, like an aerocapture maneuver, it could use a comparatively tiny scoop to collect a lot of gas, so overall the diver scoop will be much smaller and lightweight compared to other designs.
 |
| If it needs more time, the scoop can perform one diver every several orbits. |
-Electrodynamic tethers
-Electric scoop
Between 60 and 1000km altitude, Earth's atmosphere stops being a continuous medium and becomes a loose plasma dominated by charged particles. This is called the ionosphere. For example, monoatomic oxygen is a negatively charged particle that represents a large fraction of gasses at 200k altitude and above.
These ions can be collected by an electromagnetic/electrostatic scoop. The electromagnetic section is composed of large magnetic fields that direct ions towards the ship from a large volume of space. It would be similar in operation to a Bussard Ramjet. The electrostatic section is composed of extremely thin rings with a charged interior. Ions of the unwanted charge are deflected, ions of the desired charge are pulled to the center, where a physical scoop collects the gas. The main advantage of this design is that it allows a tiny scoop and a set of magnets to do the work of a much larger funnel.
 |
| An interstellar voyage by the Bussard Ramjet |










As for power: you could beam power from a higher orbit (little to no drag) to your scoop. This craft in higher orbit could also store and proces everything the scoop gathers. This way, cargo haulers don't need to dock with the scoop (and the scoop can keep scooping), but can dock with a constantly available store of gathered material.
ReplyDeleteDefinitely! Since you only need to climb to an altitude of 400km or so for drag to becomes extremely low, you can skip lasers, which are most useful at extreme ranges, and use much simpler solar concentrators.
DeleteThese are concave disks of aluminium on a swiveling mount. They focus sunlight down to the scoop ship at 200km altitude. This allows the scoop ship to use tiny photovoltaic panels.
Of course, you'd need several concentrator satellites, but they are very lightweight and would be cheap to make.
Conventional scoops that stick to a single low altitude are best services by shuttles or OTVs that simply launch into their inclination and dock with them, which saves on propellant otherwise needed to transfer between the scoop's orbit and the spaceship's parking orbit. Scoops continue working even when docked to another craft.
Only a 'diver' design would benefit from cargo being collected at a different orbit.
Hi! Great article!
ReplyDeleteA little nitpick – you wrote "the only way of delivering propellant to a spaceship in orbit is with another launch. This negates any direct advantage refueling provides." Which not necessarily be show-stopper. Various schemes include orbital propellant depot constantly refueling using same space gun/mass driver that shot small propellant tanks into space.
The spaceship could be launched empty and fueled at the depot. Humans are fragile and could not survive the high G acceleration the mass driver produce and unlike the tanks could not be split into smaller units to be load and launch separately like the propellant can.
Yoel
I should have clarified: currently. We don't have a moon base or a captured asteroid yet, so we can only put things into orbit by dragging them up from the ground.
DeleteIf I understand correctly, you are proposing to send dumb payloads into orbit by accelerating them close to orbital velocity, from the ground, by railgun? The idea has some merit and has been studied closely.
Never claim this arrangement is my own design, but this is my original:
DeleteI have an idea for In-situ concept better than mining asteroids and/or the moon or scooping the higher atmosphere for extraction of propellant in order to fill orbital propellant depots.
Place a magnetic sail at one of the stable Lagrangian points (L4 & L5) for harvesting solar wind. A magnetic loop will form a magnetic 'scoop' as in the theoretical Bussard ramjet. The Bussard ramjet concept relay upon moving vessel at somewhere between 1% to 6% of light speed to compressed interstellar hydrogen to fusion pressure and temperatures.
The solar wind is racing at 300km/s or only 0.1% of C against a stationary object at Lagrangian point which should be enough to compress the solar wind, mostly hydrogen, into the propellant tanks.
Lagrangian point is stable enough that the satellite won't be drove out of it by the force applied by the solar wind.
An unmanned propellant 'tankers' will drive the propellant from the Lagrangian point/s to satellites and spaceships refueling at LEO & GEO and back to L4 & L5 on an endless cycling.
What do you think?
Yoel
Sorry for the late reply.
DeleteThe idea is sound... if the solar wind could be exploited practically.
The solar wind contains about 3 million particles per cubic meter. The majority is hydrogen, so this represents 5e-19kg per cubic meter. At a velocity of 495km/s, you might be able to intercept 2.48e-15kg per second per square meter.
The advantage is that the stream is mostly composed of ions that are easily manipulated by a magnetic field. The downside is that in Earth's upper atmosphere, even at 400km altitude, you'll be able to collect ten million times more mass per square meter.
The x10000000 difference is on top of saving on whatever propellant is needed to move the tankers between the Lagrangian points and wherever it is needed.
Using a magnetic scoop 400km in diameter, a solar wind scoop can extract 26.9kg of solar wind particle per day.
DeleteIt maybe useful at some stars with strong stellar wind or very close range only.
I see it as the method to mine gas giants for fusion fuel, rather than scooping fuel for chemical rockets.
ReplyDeleteCan the electric scoop still work in lower altitudes and combine it with the trawler design?
Totally OT, but related to your interstellar series: http://www.kschroeder.com/my-books/permanence/the-cycler-compact.
ReplyDeleteThere is some confusing text where it looks like you did 'cut & paste' wrong.
ReplyDeleteShortly before the subtitle "What's the point of all this?" there is some text about the 'diver' concept which seems to belong farther down.
I must have hit publish without properly reviewing that all the draft notes were gone!
ReplyDeleteI particularly like the idea of putting the scoop on the low end of an electrodynamic tether. This would have the complication that, since the force from the tether is perpendicular to the magnetic field ie: within a few degrees of eastward, the tether scoop combination will end up orbiting within a few degrees of the equator, regardless of the initial inclination. So the launch site for access to the scoop will have to be almost on the equator. I'm not sure if even the French Guiana launch site is close enough to the equator.
ReplyDeleteHowever, this will have the advantage noted here:
http://www.nss.org/settlement/space/GlobusEasierSettlement.pdf
that right over the equator is where you want an inhabited space station, since that is where radiation levels are low enough for indefinite habitation with minimal shielding.
So people might want to put up an electrodynamic tether a few km long, with a scoop at the low end, a space station near the middle, & the power supply, either solar or nuclear, at the top. Rockets from an equatorial launch site would deliver comsats, interplanetary space probes, etc. to the bottom of the tether, & the astronauts in the space station would put propellant in the spacecraft & make sure they had taken no damage from launch before sending them onward.
A scheme like this would also mean that spacecraft could be assembled at this space station from components launched separately.
By requirement, the scoop will be equipped with a very high Isp engine. Loading up the scoop with a bit of propellant before it is launched will give it a very good deltaV capacity, enough to make plane changes trivial.
DeleteIf you exclusively use a tether for propulsion, then just launch it into a convenient plane and extend the tether without scooping to push it towards the equator over time.
Personally, I do not think gas scoops should be tied to space stations. To me, it is the equivalent of adding a hotel to every oil rig in the North Sea. It might have some use, but we'd be better off just separating the functions. If a space station is needed for assembly, they still would not have to share a tether after the assembly is complete.
The fact is, gas scoops are inherently unstable and a system failure will eventually cause it to get dragged down into the atmosphere and burn up. If the scoop funnel is stuck in an extended position following a propulsion failure, the scoop can come down and burn up in a matter of hours and days - this is not a failure mode you want to have a space station stuck with.
The purpose of having the electrodynamic tether is to provide the high ISP propulsion, and such a tether will likely need a ballasting weight on the far end, so making it a functional item like a space station makes sense.
DeleteAs for failure modes. the space station can take steps like reeling in the tether to bring a malfunctioning scoop out of the atmosphere, or in an extreme emergency cutting the tether and letting the scoop fall into the atmosphere.
Another advantage I can see is to simplify the entire process. The station controls the altitude of the scoop, and once the scoop has filled its tanks the station reels it in and either unloads the product, fuels a space ship or swaps out the full tank for an empty and sends it back on its way for another pass through the atmosphere. The scoop can be largely a passive device, with much of the work being done higher up on the station.
I'm not certain about this, but instead of having the scoop ship hand on one long tether, how about a 'skirt' of multiple shorters tethers stretched outwards by centripetal force for propulsion? No need for a counterweight then.
DeleteI'll admit I'm not certain either, but AFAIK the energy and propulsion potential of the tether is related to the length of the device. One long tether should b e much more efficient or powerful (depending on if you are harvesting energy or using it for propulsion) than multiple short ones.
DeleteSo simplifying it as far as possible, you have a scoop at one end of a long tether, and a you terweight at the other end in higher orbit. This carries the solar panels, reel mechanism and possibly a tank swapping facility (when the scoop has filled a tank it is brought up, and the full tank swapped for an empty tank). A fuelling facility for spacecraft is provided at the "top" of the assembly, and it would make sense for at least a limited inspection and repair facility as well, even if it is just a robot giving the scoop a quick once over before lowering it.
I've looked into the equations which determine electrodynamic tether performance and it looks like they are independent of length: two short wires are the same as one long wire. However, the electromagnetic field around the wires deflects ions in Earth's magnetosphere and sprays them out in all directions. Having two tethers close to each other will cause interference. There's also the question of the angle of the tether in relation to the direction of travel and the gravity gradient. It will be pulled vertical over time unless enough centripetal force is applied.
DeleteFor a scoop at the low end of a tether, how would the extracted product be sent upward? Would a small pressure-fed pipe be enough? How light and thin can it be made? What are the failure mods (e.g. a leak) and how do we cope with them?
ReplyDeleteThe pressure gradient should be large enough to counter-act gravity and allow for fast enough pumping rates in necessarily thin tubes.
DeleteEven enormous gas scoops in lower orbits will only be collecting a few grams per second, so the pressure gradient required to continuously move the gas collected is very very small - the transfer tube would probably end up being paper thin with just enough self-sealing ability to handle the one or two micrometeorites it hits per year.
Might find this interesting:
ReplyDeletehttps://www.nextbigfuture.com/2017/09/higher-power-and-high-density-nuclear-electric-for-space-missions.html
Very interesting propulsion concept, thanks!
DeleteI note that you would separate the nitrogen & oxygen by fractional distillation. Has anyone figured out a way to make this work in micro-gravity? Would putting the scoop on a *long* tether be needed to get enough gravity for the distillation to work. perhaps the distillation would have to be done on a rotating subsystem.
ReplyDeleteInstead what other ways of separating air components are there that might be more practical in space?
You can use a small centrifuge to separate the fluids, or a cooled capillary action surface that drains away liquids that condense on its surface.
DeleteI have not yet had time to read through the entire article, but there is an important aspect of the VASIMR calculations that needs to be corrected. Notably, I am refering to your statement that, "(w)e can work out that each kW of electrical power supplied to the RF plasma thruster produces 0.052N of thrust out of 1.72kg of engine".
ReplyDeleteThese figures are based on rather specific assumptions, and might tend to misconstrue the actual data.
*IIRC (I am relying totally on my recollection of the VASIMR data presented in a number of research papers... I might be confusing specific elements), the thrust value of 52mN/kW is baed on data for Argon propellant at approximately 1600s Isp (I think it might actually be 1660s, or maybe 1680s... it might even be as high as 1860s, if I am inverting a couple digits in my memory, but it is not any higher). This is the peak thrust/power value. From there it drops again to about 25mN - 30mN per kW, as you increase Isp.
*I might be mistaken, but I seem to recall that the 60% efficiency was obtained at above 4000s Isp, again with Argon. So, that value from the same paragraph would not be valid with the rest of the data.
*One of the features of VASIMR is that the thruster mass does not scale proportionately with power. Again, IIRC, the 1.7kg/kW engine mass figure is dependent on power levels of AT LEAST 200kW. Most of the mass of the VASIMR engine is constant. As I understand it, the actual production model is meant to have approximately the same component mass and size of the VX200 test model, but will actually be able to support in excess of 10MW (once the thermal waste removal components are installed). On the one hand, this means that the actual mass/power ratio will be much lower than 1kG/kW throughout the nominal power range. On the other hand, it also means that the ratio will be rather attrocious at low power (it is no longer competitive with other electric thrusters once below about 40kW). AdAstra is developing a special model specifically for the low power range, but (once again, IIRC) even here it is unlikely that the thruster mass will ever get below a few hundred kg.
Hi Mikkel!
DeleteI agree, the data on power-to-weight ratios of most technologies in development or in testing is very sparse, and you point out that even the numbers that are available do not scale well.
I used a combination of power to weight ratio (W/kg) and the rocket power output equation (Power=Ex.Velocity*Thrust/2) to work out an approximate thrust to weight ratio.
The design I came up with used about 250kW for propulsion, so it should be within the ballpark of the power ratings the numbers on VASIMR are for.
But, in the overall scheme, the system mass is only relevant when you want to find out how much you could save based on the payload of a rocket, in this case a Falcon 9 putting 22.8 tons into LEO. The actual performance of the gas scoop does not depend on mass at all!
Yes, the numbers would probably apply pretty well for 250kW, assuming the "low gear" you specified. I was more concerned that someone might (mis)interpret your statements, and think that a smaller, "personalised", craft might get away with a 10 kG thruster, just because it is design to only need a few mN of thrust to perform a certain mission.
ReplyDeleteBTW: technically, the performance of the gas scoop DOES depend on mass. However, this mass factor is already taken into consideration when calculating drag, etc (specifically, the drag on the ship is the result of accelerating the mass of gas molecules the ship comes into contact with... the mass continues to exert drag until the molecules are either pushed out of the way, or are accelerated to the same velocity as the craft). I think it might also be important to clarify that your statement only applies to thrust performance. Required duration of thrust WILL be dependent upon mass, although this, too, could probably be accounted for in the drag equations, if they are configured properly.
>Required duration of thrust WILL be dependent upon mass, although this, too, could probably >be accounted for in the drag equations, if they are configured properly.
ReplyDeleteAre you referring to the complications of intermittent use of the thrusters? I specifically chose continuous thrusting/perfectly circular orbit/continuous operation for the simplicity of the calculations.
"Are you referring to the complications of intermittent use of the thrusters? I specifically chose continuous thrusting/perfectly circular orbit/continuous operation for the simplicity of the calculations."
DeleteNo.
I mean that the amount of mass you collect will determine how long you have to burn (whether continuously or otherwise... although the specific burn time will also be affected by these factors as well) under a given thrust in order to achieve (or return to) a given orbit. However, again, much of this mass effect will be built-in to the drag calculations, meaning that you will not have to address the mass component separately. What I am saying, however, is that IF you don't configure the drag calculations correctly (for instance, only factoring in the drag during atmospheric traverse, instead of taking the drag into account throughout the "mission") you might have to factor in that mass separately later in the flight equations.
*Normally, you SHOULD not have to figure in the platform mass, because momentum is conserved. All that you need to do for the platform alone is to balance out the "deorbit" burn with the recovery burn, directly.
*Any loss of momentum for the platform will be do to drag while passing through the atmosphere, so balancing out the drag will automatically balance out this loss of momentum. So, again, you do not need to factor the platform mass in a separate equation.
*Drag, ITSELF, will factor in the mass of the atmospheric gases (either directly or indirectly, depending upon the equations used). This means that you don't have to factor the mass in separately.
**Importantly, IF your calculations for drag take into account the target delta-V, then you should not need to factor in mass separately. HOWEVER, again, if your drag calculations only factor in resistance of mass as the platform passes through the atmosphere, then you WILL need to factor the mass of actual collected material in order to determine the amount of momentum you need to add through an additional duration of thrust in order to achieve a desired orbit.
Crowlspace has a post about using the SpaceX BFR architecture to reach Saturn in a fairly reasonable 3 year timeframe using all chemical rockets. This can tie into the atmospheric scooping to some extent since both the BFR and Musk's earlier musings about going to Mars required the spacecraft to meet with a refuelling tanker in LEO to complete the journey.
ReplyDeleteWhile lofting hundred ton+ tanks of propellant and oxidizer may seem a daunting task (personally, I'd use something even cheaper and simpler like "Sea Dragon" to loft tanks of fuel and oxidizer into orbit, but that's me), being able to scoop the oxidizer out of the atmosphere and process it on the spot (so to speak) makes sense when coupled to the BFR architecture. Now fewer launches are needed to assemble the stack for a voyage to Mars or Saturn, or a smaller Falcon or Falcon heavy can be used to bring the propellant and the oxidizer simply transferred from the scoop assembly.
For more of the BFR and its ability to make a deep space voyage, see http://crowlspace.com/?p=2900
For comparison, if we put a 150 ton scoop with advanced materials and 10kW/kg electric components into orbit, we can pulling in over 6200 tons of liquid oxygen per year.
DeleteThat's enough to fill the liquid oxygen tanks of 7.2 BFRs. Instead of taking 7.33 refueling flights of 150 tons of propellant cargo to fill 1100 tons in an empty BFR in orbit, you can fill up all the liquid oxygen at once and bring up only two cargo bays of liquid methane to provide the rest.
Alternatively, fill up a fleet of seven BFRs with liquid oxygen and only require 11.2 launches of liquid methane to fill up the rest.
And all that with only one BFR launch dedicated to a 0.428kg/m^2 scoop and no further optimisation.
Has anything more recent than the PROFAC suggestion been done about this idea? I love the idea but I would be less skeptical if I could find more than 1 blog post on it. A paper in an engineering journal would get more serious scrutiny for flaws in the idea. Some actual construction & experimentation would be even better.
ReplyDeleteI'm sorry, I couldn't even find PROFAC until it was mentioned to me.
DeleteI did some work on this idea while working on my space systems engineering textbook:
Deletehttps://en.wikibooks.org/wiki/Space_Transport_and_Engineering_Methods/Resource_Extraction#Mining_Atmospheres
There are a couple of references I found. One note about the scoop ship concept:
Average molecule velocity @ 200 km is about 1 km/s, and orbit velocity is about 8 times this. At this altitude molecules act independently at the scoop altitude, and simply bounce off the scoop surface. You therefore need a highly inclined scoop surface so they don't bounce back out. Towards the back of the funnel, the sideways motions imparted to to molecules brings their density to the point they hit each other, rather than just the walls. You get a stagnation shock at this point, where the density and temperature rises. From behind that point, you can pump the gas out, then cool it.
Thanks. I used that link as a resource for this blog post.
DeleteThe other way of getting around this is to get away from systems which need reaction mass to begin with.
ReplyDeleteBoosting payloads and hooking them up to solar sails (or variations like lightsails powered by a laser, magsails or electric sails) is low cost and actually quite fast (high performance sails such as the ones developed by K Eric Drexler have been calculated of being capable of reaching Pluto in as little a 3 years, although a flight like the would need to lithobrake in order to stop there).
More realistically, sails could make elliptical orbits to target planets, and use techniques like dropping off cargos and letting them aerobrake or decelerate using planetary magnetic fields (n the case of Jupiter and the gas giants).
This is not to say that atmospheric scooping cold not be useful, but we should always be looking for alternatives which may be faster, cheaper or otherwise less resource intensive for the user.
I can imagine a transport network that uses high Isp solar electric engines, atmospheric scooping and orbital tethers to completely do away with the need to supply propellant.
DeleteThe solar electric engines fill themselves in LEO and take payloads to their destination, where they are brought to the ground by an orbital tether. The tether drags up some propellant on the upwards spin and uses it to boost itself back into position. Meanwhile the solar electric craft returns itself to LEO and refills itself.
Elegant?
It looks like part of the technology for this is being developed.
ReplyDeletehttps://www.nextbigfuture.com/2018/03/how-low-orbit-can-satellites-go.html
There's one thing that confuses me about your analysis here--the statement that no active pumping will be required because the funnel alone will suffice to pump it. By my count, the stagnation pressure will still be a lot lower than the triple point of nitrogen--so you'd need some active compression after your first ramming step to liquefy it at all. Is the calculation for stagnation pressure different with rarefied gasses, or does this design exercise actually need to take into account the power needed to compress the gas?
ReplyDeleteI'll clarify my statement:
DeleteThere are three components that the molecules that are scooped up go through - the funnel, a capture tank and long term storage.
The funnel rams molecules into a put at the bottom with a stagnation pressure. The pit opens into a capture tank. The capture tank is held at a lower pressure than the stagnation pressure, which is achieved by it being mostly empty.
The pressure difference allows the molecules, in gaseous form, the flow into the capture tank with no active pumping needed.
A valve then closes off the capture tank.
The capture tank's contents are then cooled until they liquefy. The condensed moleculares are pumped into a long-term storage tank, leaving the capture tank empty.
The valve then opens again, allowing the funnel to be emptied into the capture tank again.
The only step which requires power input is the rapid cooling and liquefaction of molecules in the capture tank. It can be done easily for something like oxygen or nitrogen, as simply mixing in liquid hydrogen cools them down to below their boiling temperature. For hydrogen and helium, it is more difficult, as you'd need rather huge heat pumps.
An ion rocket with exhaust velocity higher than orbital or a tether getting momentum for Lorentz force would take a lot of juice. Which means lots surface are. Either surface in the form of solar panels or, if nuclear, lots of radiator surface to dump waste heat.
ReplyDeleteLots of surface area makes for momentum loss as you're passing through the upper atmosphere. Perhaps the solar panels or radiator could also form the scoop?
An electrodynamic tether needs to be in the ionosphere so as to complete the circuit. During times it's at a high apogee it would not be able to enjoy Lorentz force.
Hi Hollister David.
DeleteI assumed throughout the blog post that either solar panels or radiators could be placed to hide within the 'shadow' of the gas scoop, and therefore not contribute to any drag greater than what the scoop causes.
If very larger solar panels or radiators are needed, they can simply be elongated to have the necessary surface area without increasing the craft's frontal cross-section.
Nice blog! You made the sort of fascinating piece to peruse, giving every subject illumination for humans to get studying. wrong fuel in hampshire
ReplyDeleteOne interesting thing to note is that, at least on Earth, at least if you have to stop all of the collected gas, a scooper is not energetically worth it vs launching the propellant from the ground, assuming a non-rocket spacelaunch method like an orbital ring is available. Specific orbital energy at LEO (relative to the ground) is about 30 MJ/kg, but a scooper, assuming it stops all the gas it collects, has 100% efficient propulsion, and is operating at the optimal exhaust velocity for minimal energy expenditure (2x the orbital velocity under these assumptions) will require about 120 MJ of propulsive energy for each kg of propellant retained.
ReplyDeleteHowever, even if the portion of the scooped gas used as propellant is allowed to retain 90% of its velocity, about 53 MJ of propulsive energy are still required for each kg of retained propellant.
So, propellant scooping for gathering propellant only makes energetic sense in the early period of a spacefaring civilisation, or for colonies around atmospheric worlds in early stages of development, before significant space-access infrastructure is built.
This also has implications for fusion fuel scooping, and means you would want to do it on the lightest gas giant available in all likelihood. On Neptune, an ideal scooper that in this case does decelerate all the gas it collects (since it is the fusion fuel we are after) requires 550 MJ per kg of gas collected, which will be about two-thirds hydrogen and one-third helium by mass. With an isotope number ratio of 4e-5 D/H (and thus an isotope mass fraction of 8e-5), and an isotope number ratio of 1.66 e-4 He3/He4 (mass ratio 1.25e-4, I am assuming this ratio is the same in Neptune as it is in Jupiter, the only gas giant for which I can find data)), we would be collecting about 53 mg of deuterium and 42 mg of He3 for each 550 MJ, for about a 1.9:1 by atom number D-He3 mix. If the He3 is fully reacted in the D-He3 reaction, this fuel would produce about 22 GJ of energy, far exceeding the amount required to collect it.
Even a Jupiter scooper, which would for each 3.5 GJ spent recover only 49 mg of deuterium and 12.5 mg of He3 (a 6:1 D-He3 number ratio) would still recover about 7.3 GJ just from reacting the He3 it collects in a D-He3 reaction, not to mention the possible further energy gain from D-D fusion.
Ah, wait, I made a mistake, forgot to convert volume to mass ratios for Jupiter's atmosphere. The Jupiter scooper would for each kg of atmosphere retained recover about 43 mg of deuterium and 23 mg of He3, for a yield of about 13.5 GJ from D-He3 fusion alone.
DeleteAnd I would like to further note that I am making the pessimistic assumption here that only the fusion fuel in the part of the scooped gas that is retained can be recovered - if the isotopic fractionation is done before the gas to be used as propellant is ejected, then the fusion fuel amounts recovered, if the exhaust velocity is chosen at twice the orbital velocity, double.
DeleteI was thinking about the trawler design for a gas scoop earlier today and was toying with the idea of the trawler rotating its scooping tether like a skyhook so that the scoop would hit the air at the bottom of its arc more slowly and have less drag. But then I realized the reduced energy loss from the reduced drag was paid for by having to fight centripetal force to pump the gases up the rotating tether. And you would still have to adjust the systems' momentum as well, cause as you pumped mass from the tip of the tether to the center of rotation the tether would spin faster, and so you would need to counter that with thrusters. But then I realized, you wouldn't necessarily need thrusters, cause if problem is the tether spinning too fast, eventually the tip of the tether at the bottom of its arc would no longer be at rest with air, it would be moving backwards, and so drag would help by slowing the tip down. I think you could actually gain a bit of orbital momentum in that way, cause the scoop would be shoving the air in the opposite direction of the trawlers orbit. The system is pushing off the atmosphere like a paddle wheel.
ReplyDeleteI just don't know if the increased spin from pumping mass from the tip to the center would balance the loss in spin from drag. I'm guessing not completely, but could maybe reduce the amount of thrusters you need. Probably not as practical as an electrodynamic tether, but seems cool. Might be useful as a propellant less propulsion option for worlds without magnetospheres, let them gain momentum by reacting against the atmosphere instead.