We work out just how effective they can be, and how they stack up against conventional electrically-powered lasers. You might want to re-think your space warfare and power beaming after this.
Nuclear energy and space have been intertwined since the dawn of the space age. Fission power is reliable, enduring, compact and powerful. These attributes make it ideal for spacecraft that must make every kilogram of mass as useful and as functional as possible, as any excess mass would cost several times its weight in extra propellant. They aim for equipment for the highest specific power (or power density PD), meaning that it produces the most watts per kilogram.
Lasers use a lasing medium that is rapidly energized or
‘pumped’ by a power source. Modern lasers use electric discharges from
capacitors to pump gases, or a current running through diodes. The electrical
power source means that they need a generator and low temperature radiators in
addition to a nuclear reactor… these are significant mass penalties to a
spaceship.
Fission reactions produce X-rays, neutrons and high energy
ions. The idea to use them to pump a lasing medium has existed ever since the
first coherent wavelengths were released from a ruby crystal in 1960.
Much
research has been done in the 80s and 90s into nuclear-pumped lasers,
especially as part of the Strategic Defense Initiative. If laser power can be
generated directly from a reactor, there could be significant gains in power
density.
The research findings on nuclear reactor lasers were
promising in many cases but did not succeed in convincing the US and Russian
governments to continue their development. Why were they unsuccessful and what
alternative designs could realize their promise of high power density lasers?
Distinction between NBPLs and NRLs
Most mentions of nuclear pumped lasers relate to nuclear bomb-pumped lasers. They are exemplified by project Excalibur: the idea was to use
the output of a nuclear device to blast metal tubes with X-rays and have them
produce coherent beams of their own.
We will not be focusing on it.
The concept has many problems that prevent it from being a
useful replacement for conventional lasers. You first need to expend a nuclear
warhead, which is a terribly wasteful use of fissile material. Only a tiny
fraction of the warhead’s X-rays, which are emitted in all directions, are
intercepted by the metal tube. From those, a tiny fraction of its energy is
converted into coherent X-rays. If you multiply both fractions, you find an
exceedingly low conversion ratio.
Further
research has revealed this to be on the order
of <0.00001%. It also works for just a microsecond, each shot
destroys its surroundings and its effective range is limited by relatively poor
divergence of the beam. These downsides are acceptable for a system meant to
take down a sudden and massive wave of ICBMs at ranges of 100 to 1000
kilometers, but not much else.
Instead, we will be looking at nuclear reactor pumped
lasers. These are lasers that draw power from the continuous output of a
controlled fission reaction.
Performance
We talk about efficiency and power density to compare the
lasers mentioned in this post. How are we working them out?
For efficiency, we multiply the reactor’s output by the
individual efficiencies of the laser conversion steps, and assume all
inefficiencies become waste heat. The waste heat is handled by flat
double-sided radiator panels operating at the lowest temperature of all the
components, which is usually the laser itself.
This will give a slightly poorer performance than what could
be obtained from a real world engineered concept. The choice of radiator is
influenced by the need for easy comparison instead of maximizing performance in
individual designs.
We will note the individual efficiencies as Er for the
reactor, El for the laser and Ex for other components. The overall efficiency
will be OE.
- OE = Er * Ex * El * Eh
In most cases, Er and Eh can be approximated as equal to 1.
As we are considering lasers for use in space with output on the order of
several megawatts and beyond, it is more accurate to use the slope efficiency
of a design rather than the reported efficiency. Laboratory tests on the
milliwatt scale are dominated by the threshold pumping power, which cuts into
output and reduces the efficiency. As the power is scaled up, the threshold
power becomes a smaller and smaller fraction of the total power.
Calculating power density (PD) in Watts per kg for several
components working with each other’s outputs is a bit more complicated. As
above, we’ll note them PDr, PDl, PDh, PDx and so on. The equation is:
- PD = (PDr * OE) / (1 + PDr (Ex/PDx + Ex*El/PDl + (1 - Ex*El)/PDh))
Generally, the reactor is a negligible contributor to the
total mass of equipment, as it is in the several hundred kW/kg, so we can
simplify the equation to:
- PD = OE / (Ex/PDx + Ex*El/PDl + (1 - Ex*El)/PDh)
Inputting PDx, PDl and PDh values in kW/kg creates a PD value
also in kW/kg.
Direct Pumping
The most straightforward way of creating a nuclear reactor
laser is to have fission products interact directly with a lasing medium. Only
gaseous lasing mediums, such as xenon or neon, could survive the conditions
inside a nuclear reactor indefinitely, but this has not stopped attempts at
pumping a solid lasing medium.
Three methods of energizing or pumping a laser medium have
been successful.
Wall pumping
Wall pumping uses a channel through which a gaseous lasing
medium flows while surrounded by nuclear fuel. The fuel is bombarded by
neutrons from a nearby reactor. The walls then release fission fragments that
collide with atoms in the lasing medium and transfer their energy to be
released as photons. The fragments are large and slow so they don’t travel far
into a gas and tend to concentrate their energy near the walls. If the channels
are too wide, the center of the channel is untouched and the lasing medium is
unevenly pumped. This can create a laser of very poor quality.
To counter this, the channels are made as narrow as possible,
giving the fragments less distance to travel. However, this multiplies the
numbers of channels needed to produce a certain amount of power, and with it
the mass penalty from having many walls filled with dense fissile fuel.
The walls absorb half of the fission fragments they create immediately. They release the surviving
fragments from both faces of fissile fuel wall. So, a large fraction of the
fission fragment power is wasted. They are also limited by the melting
temperatures of the fuel. If too many fission fragments are absorbed, the heat
would the walls to fail, so active cooling is needed for high power output.
The FALCON experiments achieved an efficiency of 2.5% when
using xenon to produce a 1733 nm wavelength beam.
Gas
laser experiments at relatively low temperatures reported
single-wavelength efficiencies as high as 3.6%. The best reported performance
was 5.6% efficiency from an Argon-Xenon mix producing 1733 nm laser light, from
Sandia National Laboratory.
Producing shorter wavelengths using other lasing
mediums, such as metal vapours, resulted in much worse performance (<0.01%
efficiency).
Higher efficiencies could be gained from a carbon monoxide or
carbon dioxide lasing medium, with up to 70%
possible, but their wavelengths are 5 and 10 micrometers
respectively (which makes for a very short ranged laser) and a real efficiency
of only 0.5%
has been demonstrated.
One estimate
presented in this
paper is a wall-pumped mix of Helium and Xenon that
converts 400 MW of nuclear power into 1 MW of laser power with a 1733 nm
wavelength. It is expected to mass 100 tons. That is an efficiency of 0.25% and
a power density of just 10 W/kg.
It illustrates the fact that designs meant to
sit on the ground are not useful
references.
A chart from this NASA report reads as a direct pumped nuclear
reactor laser with 10% overall efficiency having a power density of about 500
W/kg, brought down to 200 W/kg when including radiators, shielding and other
components.
Volumetric
pumping
Volumetric
pumping has Helium-3 mixed in with a gaseous lasing medium to absorb neutrons
from a reactor.
Neutrons are quite penetrating and can traverse large volumes
of gas, while Helium 3 is very good at absorbing neutrons. When Helium-3
absorbs neutrons, it creates charged particles that in turn energize lasing
atoms when they enter into contact with each other. Therefore, neutrons can
fully energize the entire volume of gas. The main advantages of this type of
laser pumping is the much reduced temperature restrictions and the lighter
structures needed to handle the gas when compared to multiple narrow channels
filled with dense fuel.
 However,
Helium-3 converts neutrons into charged particles with very low efficiency,
with volumetric pumping experiments reporting 0.1 to 1% efficiency overall. This
is because the charged particles being created contain only a small portion of
the energy the Helium-3 initially receives.
However,
Helium-3 converts neutrons into charged particles with very low efficiency,
with volumetric pumping experiments reporting 0.1 to 1% efficiency overall. This
is because the charged particles being created contain only a small portion of
the energy the Helium-3 initially receives.
Semiconductor
pumping
The final
successful pumping method is direct pumping of a semiconductor laser with
fission fragments. The efficiency is respectable at 20%, and the compact laser
allows for significant mass savings, but the lasing medium is quickly destroyed
by the intense radiation. It consists of a thin layer of highly enriched
uranium sitting on a silicon or gallium semiconductor, with diamond serving as
both moderator and heatsink.
A
space-optimized semiconductor design from this
paper that suggests that an overall power density of 5
kW/kg is possible. It notes later on that even 18 kW/kg is achievable. It is
unknown how the radiation degradation issue could be solved and whether this
includes waste heat management equipment. Without an operating temperature and
a detailed breakdown of the component masses assumed, we cannot work it out on
our own.
Other direct
pumped designs
Wall or
volumetric pumping designs were conceived when nuclear technology was still new
and fission fuel had to stay in dense and solid masses to achieve criticality.
More modern advances allow for more effective forms for the fuel to take. The lasing medium
could be made to interact directly with a self-sustaining reactor core. This
involves mixing the lasing medium with uranium
fluoride gas, uranium aerosols, uranium vapour at very high
temperatures or uranium micro-particles at low temperatures.
The lasing medium
could be made to interact directly with a self-sustaining reactor core. This
involves mixing the lasing medium with uranium
fluoride gas, uranium aerosols, uranium vapour at very high
temperatures or uranium micro-particles at low temperatures.
 The lasing medium
could be made to interact directly with a self-sustaining reactor core. This
involves mixing the lasing medium with uranium
fluoride gas, uranium aerosols, uranium vapour at very high
temperatures or uranium micro-particles at low temperatures.
The lasing medium
could be made to interact directly with a self-sustaining reactor core. This
involves mixing the lasing medium with uranium
fluoride gas, uranium aerosols, uranium vapour at very high
temperatures or uranium micro-particles at low temperatures.
The trouble with
uranium fluoride gas and aerosols or micro-particles is the tendency for them
to re-absorb
the energy (quenching) of excited lasing atoms. This has
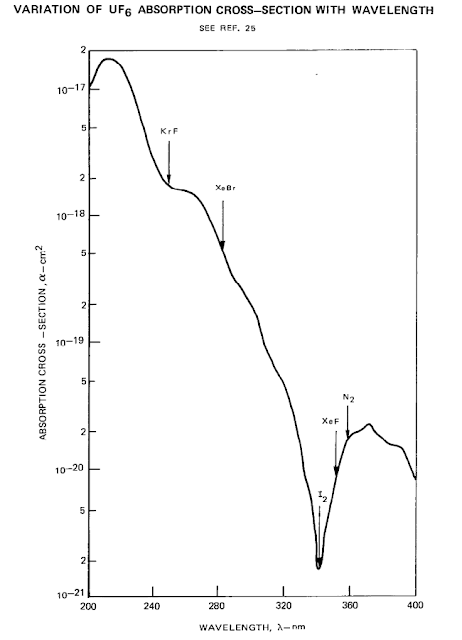
prevented any lasing action from being realized in all experiments so far. As this
diagram shows, uranium fluoride gas absorbs most
wavelengths very well, further reducing laser output.
If there is a
lasing medium that is not quenched by uranium fluoride, then there is potential
for extraordinary performance.
An early NASA
report on an uranium fluoride reactor lasers for space
gives a best figure of 73.3 W/kg from what is understood to be a 100 MW reactor
converting 5% of its output into 340 nanometer wavelength laser light. With the
radiators in the report, this falls to 56.8 W/kg.
If we bump up
the operating temperature to 1000K, reduce the moderator to the 20cm minimum,
replace the pressure vessel with ceramics and use more modern carbon fiber
radiators, we can expect the power density of that design to increase to 136
W/kg.
Uranium vapours
are another option. They require temperatures of 4000K and upwards but if the
problem of handling those temperatures is solved (perhaps by using actively
cooled graphite containers), then 80%
of the nuclear output can be used to excite the lasing medium, for an
overall efficiency that is increased four-fold over wall pumping designs.
More speculative is encasing uranium inside a C60
Buckminsterfullerene sphere. Fission fragments could exit the sphere while also
preventing the quenching of the lasing material. This would allow for excellent
transmission of nuclear power into the lasing medium, without extreme
temperature requirements.
Nuclear-electric
comparison
With these
numbers in mind, it does not look like direct pumping is the revolutionary
upgrade over electric lasers that was predicted in the 60s.
Turbines,
generators, radiators and laser diodes have improved by a lot, and they deliver
a large fraction of a reactor’s output in laser light. We expect a
space-optimized nuclear-electric powerplant with a diode laser to have rather
good performance when using cutting edge technology available today.
With a 100 kW/kg
reactor core, a 50% efficient turbine at 10 kW/kg, an 80% efficient electrical
generator at 5 kW/kg, powering 60% efficient
diodes at 7 kW/kg and using 1.34 kW/kg radiators to
get rid of waste heat (323K
temperature), we get an overall efficiency of 24% and a
power density of 323 W/kg.
A more advanced system using a very powerful 1 MW/kg reactor core, a 60% efficient MHD generator at 100 kW/kg with 1000K 56.7 kW/kg radiators, powering a 50% efficient fiber laser cooled by 450K 2.3 kW/kg radiators, would get an overall efficiency of 30% and a power density of 2.5 kW/kg.
Can we beat these
figures with reactor lasers?
Indirect pumping
The direct pumping method uses the small fraction of a
reactor’s output that is released in the form of neutrons, or problematic
fission fragments. Would it not be better to use the entire output of the
nuclear reaction?
Indirect pumping allows us to use 100% of the output in the
form of heat. This heat can then be converted into laser light in various ways.
Research and data for some of the following types of lasers
comes from solar-heated
designs that attempt to use concentrated sunlight to
heat up an intermediate blackbody that in turn radiates onto a lasing medium.
For our purposes, we are replacing the heat of the Sun with a reactor power
source. It is sometimes called a ‘blackbody laser’ in that case.
Blackbody radiation pump
At high temperatures, a blackbody emitter radiates strongly
in certain wavelengths that lasing materials can be pumped with. A reactor can
easily heat up a black carbon surface to temperatures of 2000 to 3000K – this
is what nuclear rockets are expected to operate at anyhow.
Some of the spectrum of a blackbody at those temperatures
lies within the wavelengths that are absorbed well by certain crystal and
gaseous lasing mediums.
Neodymium-doped Ytrrium-Aluminium-Garnet (Nd:YAG)
specifically is a crystal lasing medium that has been thoroughly investigated
as a candidate for a blackbody-pumped laser. It produces 1060 nm beams.
Efficiency figures vary.
A simple single-pass configuration results in very poor
efficiency (0.1 to 2%). This is because the lasing medium only absorbs a small
portion of the entire blackbody spectrum. In simpler terms, if we shine
everything from 100 nm to 10,000 nm onto a lasing medium, it will convert 0.1
to 2% of that light into a laser beam and turn the rest into waste heat. With
this performance, blackbody pumped lasers are no better than direct pumped
reactor laser designs from the previous section.
Instead, researchers have come up with a way to recover the
99 to 99.9% of the blackbody spectrum that the lasing medium does not use. This
is the recycled-heat blackbody pumped laser.
An Nd:YAG crystal sits inside a ‘hot tube’. Blackbody
radiation coming from the tube walls passes through the crystal. The crystal is
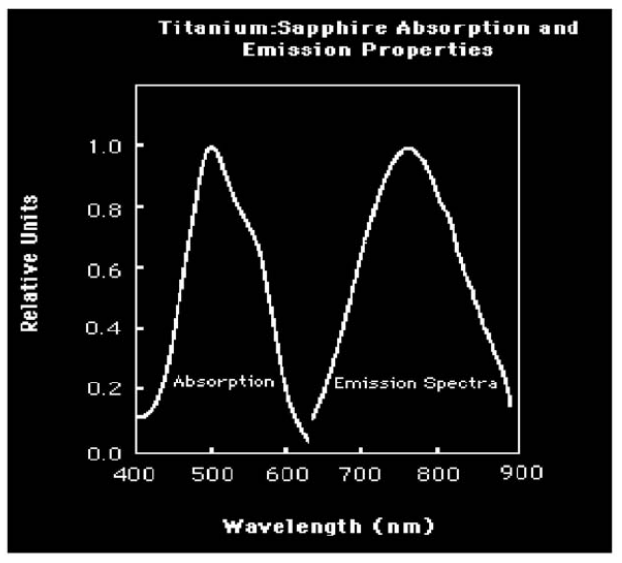
thin and nearly transparent to all wavelengths. The illustration above uses Ti:Sapphire but the concept is the same for any laser crystal.
Only about 2% of blackbody spectrum is absorbed with every
pass through the crystal. The remaining 97 to 98% pass through to return to the
hot tube’s walls. They are absorbed by a black carbon surface and recycled into
heat. Over many radiation, absorption and recycling cycles, the fraction of
total energy that becomes laser light increases for an excellent overall
efficiency.
35%
efficiency with a Nd:YAG laser was achieved.
The only downside is that the Nd:YAG crystal needs intense radiation
within it to start producing a beam. The previous document suggests that 150
MW/m^3 is needed. Another
source indicates 800 MW/m^3. We also know that
efficiency increases with intensity. If we aim for 1 GW/m^3, which corresponds
to 268 Watts shining on each square centimetre of a 1 cm diameter lasing rod,
we would need a 1:1 ratio of emitting to receiving area if the emitter has a
temperature of at least 2622K.
From a power conversion perspective, a 98% transparent
crystal that converts 35% of spectrum it absorbs means it is only converting
0.7% of every Watt of blackbody radiation that shines through it. So, a crystal
rod that receives 268 Watts on each square centimetre will release 1.87 W of
laser light.
We can use the 1:1 ratio of emitter and receiver area to
reduce weight and increase power density. Ideally, we can stack emitter and
receiver as flat surfaces separated by just enough space to prevent heat
transfer through conduction.
Reactor coolant channels, carbon emitting surface (1cm),
filler gas, Nd:YAG crystal (1cm) and helium channels can be placed back to
back. The volume could end up looking like a rectangular cuboid, interspaced by
mirror cavities.
20 kg/m^2 carbon layers and 45.5 kg/m^2 crystal layers that
release 1.87 W per square centimetre, with a 15% weight surplus for other
structures and coolant pipes, puts this component’s power density at about 250
W/kg.
The laser crystal is cooled from 417K according to the set-up in
this paper. Getting rid of megawatts at such a low
temperature is troublesome. Huge radiator surface areas will be required.
As we are using flat panel radiators throughout this post, we
have only two variables: material density, material thickness and operating
temperature. The latter is set by the referenced document.
We will choose a 1mm thick radiator made of low
density polyethylene. We obtain 0.46 kg/m^2 are plausible. When
radiating at 417K, they could achieve 3.73 kW/kg.
It is likely that they will operate at a slightly lower
temperature to allow for a thermal gradient that transfers heat out of the
lasing medium and into the panels, and the mass of piping and pumps is not to
be ignored, but it is all very hard to estimate and is more easily included in
a 15% overall power density penalty for unaccounted-for components.
A 100 kW/kg reactor, 250 W/kg emitter-laser stack and 3.73
kW/kg radiators would mean an overall power density of 188 W/kg, after applying
the penalty.
Gaseous lasing mediums could hold many advantages over a
crystal lasing medium. They require much less radiation intensity (W/m^3) to
start producing a laser beam. This
research states that an iodine laser requires 450 times
less intensity than an equivalent solid-state laser. It is also easier to cool
a gas laser, as we can simply get the gas to flow through a radiator. On the
other hand, turbulent flow and thermal lensing effects can deteriorate the
quality of a beam into uselessness.
No attempts have been reported on applying the heat recycling
method from the Nd:YAG laser to greatly boost efficiency in a gas laser. Much
research has been performed instead on direct solar-pumped lasers where the
sunlight passes through a gaseous medium just once.
The Sun can be considered to be a blackbody emitter at a
temperature of 5850K. Scientists have found the lasing mediums best suited to
being pumped by concentrated sunlight – they absorb the largest fraction of the
sunlight’s energy.
That fraction is low in absolute terms, meaning poor overall
performance. An iodine-based
lasing medium reported 0.2% efficiency. Even worse efficiency of 0.01% was achieved when using an optically-pumped bromine
laser. Similarly, C3F7I, an iodine molecule which produces 1315 nm laser light,
was considered the best at 1% efficiency.
Solid blackbody emitters are limited to temperatures just
above 3000K. There would be a great mismatch between the spectrum this sort of
blackbody releases and the wavelengths the gaseous lasing mediums cited above
require. In short, the efficiency would fall below 0.1% in all cases.
One final option is Gallium-Arsenic-Phosphorus Vertical
External Cavity Surface Emitting Laser (VECSEL) designed for use in
solar-powered designs. It can absorb wavelengths between 300 and 900nm, which
represents 65% of the solar wavelengths but only 20% of the radiation from a
3000K blackbody. This works out to an emitter with a power density of 45.9
kW/kg.
The average efficiency is 50% when producing a 1100nm beam.
Since it is extracting 20% of the wavelengths from the emitter, this amounts to
10% overall efficiency.
Using the numbers in this
paper, we can surmise that the VECSEL can handle just
under 20 MW/kg. The mass of the laser is therefore negligible. With a 100 kW/kg
reactor, we work out a power density of 3.1 kW/kg.
VECSELs can operate at high temperatures, but they suffer
from a significant
efficiency loss. We will keep them at 300K at most. It is very
troublesome as 20 MW of light is needed to be concentrated on the VECSEL to
start producing a laser beam. 90% of that light is being turned into waste heat
within a surface a few micrometers thick. Diamond heatsink helps in the short
term but not in continuous operation.
Radiator power density will suffer. Even lightweight plastic
panels at 300K struggle to reach 1 kW/kg. When paired with the previous
equipment and under a 15% penalty for unaccounted for components, it means an
overall power density of 91 W/kg.
This illustrates why an opaque pumping medium is unsuitable
for direct pumping as it does not allow for recycling of the waste heat.
Filtered blackbody pumping
A high temperature emitter radiates all of its wavelengths into
the blackbody-pumped lasing medium. We described a method above for preventing
the lasing medium from absorbing 98 to 99.9% of the incoming energy and turning
it immediately into waste heat. The requirement was that the lasing medium be
very transparent to simply let through the unwanted wavelengths.
However, this imposes several design restrictions on the
lasing medium. It has to be thin, it has to be cooled by transparent fluids,
and it might have to sit right next to a source of high temperature heat while
staying at a low temperature itself.
We can instead filter out solely the laser pumping
wavelengths from the blackbody spectrum and send those to the lasing medium
while recycling the rest.
The tool to do this is a diffraction grating. There are many
other ways of extracting specific wavelengths from a blackbody radiation
spectrum, such as luminescent dyes or simple filters, but this method is the
most efficient.
Like a prism, a diffraction grating can separate out
wavelengths from white light and send them off in different directions. For
most of those paths, we can put a mirror in the way that send the unwanted
wavelengths back into the blackbody emitter. For a small number of them, we
have a different mirror that reflects a specific wavelength into the lasing
medium.
A lasing medium that receives just a small selection of
optimal wavelengths is called optically pumped. It is a common feature of a large
number of lasers, most notably LED-pumped designs. We can use them as a
reference for the potential performance of this method.
We must note that while we can get high efficiencies, power
is still limited, as in the previous section. Extracting a portion of the
broadband spectrum that the lasing medium accepts also means that power output
is reduced to that portion.
Another limitation is the temperature of the material serving
as a blackbody emitter. The nuclear reactor that supplies the heat to the
emitter is limited to 3000K in most cases, so the emitter must be at that
temperature or lower (even if a carbon emitter can handle 3915K at low
pressures and up
to 4800K at high pressures, while sublimating rapidly).
Thankfully, the emission spectrum of a 3000K blackbody
overlaps well with the range of wavelengths an infrared fiber laser can be
pumped with.
A good example is an erbium-doped lithium-lanthanide-fluoride
lasing medium in fiber lasers. We could use it to produce green light as pictured above, but invisible infrared is more effective.
As we can see from here, erbium absorbs wavelengths between 960 and 1000 nm
rather well. It re-emits them at 1530 nm wavelength laser light with an
efficiency reported to be 42% in the ‘high Al content’ configuration, which is
close the 50% slope efficiency.
In fact, the 960-1000 nm band represents 2.7% of the total
energy emitted. It is absorbing 125 kW from each square meter of emitter. If
the emitter is 1 cm thick plate of carbon and the diffraction grating, with
other internal optics needed to guide light into the narrow fiber laser, are
90% efficient, then we can expect an emitter power density of about 5.6 kW/kg.
Another example absorbs 1460
to 1530 nm light to produce a 1650 nm beam. This is 3.7% of
the 3000K emitter’s spectrum, meaning an emitter power density of 7.7 kW/kg.
The best numbers come from ytterbium
fiber lasers. They have a wider band of wavelengths that can
be pumped with, 850
to 1000 nm (which is 10.1% of the emitter’s output), and
they convert it into 1060 nm laser light with a very high efficiency (90%). It
would give the emitter an effective power density of 23.4 kW/kg. More
importantly, we have
examples operating at 773K.
The respected
Thorlabs manufacturer gives information about the fiber
lasers themselves. They can handle 2.5 GW/m^2 continuously, up to 10GW/m^2
before destruction. Their largest LMA-20 core seems to be able to handle 38 kW/kg
of pumping power. It is far from the limit.
Based on numbers provided by this
experiment, we estimate the fiber laser alone to be on the
order of 95kW/kg. Another
source works out a thermal-load-limited fiber laser
with 84% efficiency to have a power density of 695 kW/kg before the polymer
cladding melts at 473K.
We can try to estimate the overall power density of a fiber
laser.
A 100 kW/kg reactor is used to heat a 23.4 kW/kg emitter, where a diffraction
grating filters out 90% of the output to be fed into a fiber laser with 90%
efficiency and negligible mass. The waste heat is handled by 1mm thick carbon
fiber panels operating at 773K for a power density of 20.2 kW/kg.
Altogether, this gives us 11 kW/kg after we include the same
penalty as before.
If it is too difficult to direct light from a blackbody
emitter into the narrow cores of fiber lasers, then a simple lasing crystal
could be used. This is unlikely, as it has already been done, even in high radiation environments.
Nd:YAG, liberated from the constraint of having to be nearly
entirely transparent, can achieve good performance. It can sustain a temperature
of 789K.
We know that Nd:YAG can achieve excellent
efficiency when being pumped by very intense 808nm light to
produce a 1064nm beam, of 62%. It is hoped that this efficiency is maintained
across the lasing crystal’s 730 to 830nm absorption band.
A 3000K blackbody emitter releases 6% of its energy in that
band. At 20 kg/m^2, this gives a power density of 13.8 kW/kg. We will cut off
10% due to losses involved in the filtering and internal optics.
As before, the laser crystal itself handles enough pumping
power on its own to have a negligible mass.
The radiators operating at 789K will require carbon fiber
panels. They’ll manage a power density of 22 kW/kg.
Optimistically, we can expect a power density of 3.7 kW/kg
(reduced by 15%) when we include all the components necessary.
Ultra-high-temperature blackbody pumped laser
We must increase the
temperature of the blackbody emitter. It can radiate more energy across the
entire spectrum, and concentrates it in a narrower selection of shorter
wavelengths.
Solid blackbody
surfaces are insufficient. To go beyond temperatures of 4000K, we must consider
liquid, gaseous and even plasma blackbody emitters. This requires us to abandon
conventional solid-fuel reactors and look at more extreme designs.
There is a synergy to
be gained though. The nuclear fuel can also act as blackbody emitter if light
is allowed to escape the reactor.
Let us consider two
very high to ultra-high temperature reactor designs that can do that: a 4200K
liquid uranium core with a gas-layer-protected transparent quartz window and a 19,000K
gaseous uranium-fluoride ‘lightbulb’ reactor.
For each design, we
will try to find an appropriate laser that makes the best use of the blackbody
spectrum that is available.
4200K:
Uranium melts at
1450K and boils at 4500K. It can therefore be held as a dense liquid at 4200K. We
base ourselves on this liquid-core nuclear
thermal rocket,
where a layer of fissile fuel is held against the walls of a drum by
centrifugal effects. The walls are 10% reflective and 90% transparent.
The reflective
sections hold neutron moderators to maintain criticality. This will be
beryllium protected by a protected silver
mirror.
It absorbs wavelengths shorter than 250 nm and reflects longer wavelengths with
98% reflectivity.
We expect the neutron
moderator in the reflective sections, combined with a very highly enriched
uranium fuel, to still manage criticality. The spinning liquid should spread
the heat evenly and create a somewhat uniform 4200K surface acting as a
blackbody emitter.
The transparent
sections are multi-layered fused quartz. It is very transparent to the wavelengths a
4200K blackbody emitter radiates – this means it does not heat up much by
absorbing the light passing through.
We cannot have the
molten uranium touch the drum walls. We need a low thermal conductivity gas
layer to separate the fuel from the walls and act like a cushion of air for the
spinning fuel to sit on. Neon is perfect for this. It is mentioned as ideal for
being placed between quartz walls and fission fuel in nuclear lightbulb reactor
designs. The density difference between hot neon gas and uranium fuel is great
enough to prevent mixing, and the low thermal conductivity (coupled with high
gas velocity) reduces heat transfer through conduction. We might aim to have
neon enter the core at 1000K and exit at 2000K.
There is still some
transfer of energy between the fuel and the walls because the mirrors are not
perfect; about 1.8% of the reactor’s emitted light is absorbed as heat in the
walls. Another 0.7% in the form of neutrons and gamma rays enters the
moderator. We therefore require an active cooling solution to channel coolant through
the beryllium and between the quartz layers. Helium can be used. It has the one
of the highest heat capacities of all simple gases, is inert and is even more
transparent than quartz.
Beryllium and silver can survive 1000K temperatures,
so that will set our helium gas temperature limit.
A heat exchanger can
transfer the heat the neon picks up to the cooler helium loop. The helium is
first expanded through a turbine. It radiates its accumulated heat at 1000K. It
is then compressed by a shaft driven by the turbine.
If we assume that the
reactor has power density levels similar to this liquid core rocket (1 MW/kg) and that 2.5%
of its output becomes waste heat, then it can act as a blackbody emitter with a
power density of 980 kW/kg. Getting rid of the waste heat requires 1 mm thick
carbon fiber radiators operating at 1400K. Adding in the weight of those
radiators and we get 676 kW/kg.
A good fit might be a
titanium-sapphire laser. It would absorb the large range of wavelengths between
400 and 650 nm.
That’s 18.5% of a
4200K emitter’s spectrum. If we use a diffraction grating to filter out just
those wavelengths, and include some losses due to internal optics, we get 125
kW of useful wavelengths per kg of reactor-emitter.
The crystal can
operate at up to 450K temperature, with 40% efficiency. Other experiments into the temperature
sensitivity of the Ti:Al2O3 crystal reveals lasing action even at 500K, with
mention of a 10% reduction to efficiency. We will use the 36% figure for the
laser to be on the safe side. Based on data from this flashpumping
experiment
and this crystal database, we know that it can
easily handle 1.88 MW/kg. The mass contribution of the laser itself is
negligible.
Any wavelengths that
get absorbed but are not turned into laser light become waste heat. At 450K
temperature, we can still use the lower density by HDPE plastic panels to get a
waste heat management solution with 4.6 kW/kg.
Putting all the
components together and applying a 15% penalty just to be conservative, we obtain
an overall power density of 2.2 kW/kg.
19,000:
If we want to go
hotter, we have to go for fissioning gases. Gas-core ‘lightbulb’ nuclear
reactors will be our model.
The closed-cycle
‘lightbulb’ design
has uranium heat up to the point where it is a very high temperature gas. That
gas radiated most of its energy in the form of ultraviolet light. A rocket
engine, as described in the ‘NASA reference’ designs, would have
the ultraviolet be absorbed by small tungsten particles seeded within a
hydrogen propellant flow. 4600 MW of power was released from an 8333K gas held
by quartz tubes, with a total engine mass of 32 tons.
We want to use the
uranium gas as a light source. More specifically, we want to maximize the
amount of energy released in wavelengths between 120 and 190 nm. 19,000K is
required. It is within reach, as is shown here.
Unlike a rocket
engine, we cannot have a hydrogen propellant absorb waste heat and release it
through a nozzle. The NASA reference was designed around reducing
waste heat to remove the need for radiators, but we will need them. Compared to
the reference design, we would have 27 times the output due to the higher
temperatures, but then we have to add the mass of the extra radiators.
About 15% of the
reactor’s output is lost as waste heat in the original design. It was expected
that all the remaining output is absorbed by the propellant. We will be having
a lasing gas instead of propellant in between the quartz tube and the reactor
walls. The gas is too thin to absorb all the radiation, so to prevent it all
from being absorbed by the gas walls, we will use mirrors.
Polished, UV-grade
aluminium can handle the UV radiation. It reflects it back through the laser
medium and into the quartz tubes to be recycled into heat. Just like the
blackbody-pumped Nd:YAG laser, we can create a situation where the pumping
light makes multiple passes through the lasing medium until the maximum
fraction is absorbed.
Based on this calculator and this UV enhanced coating, we can say that
>95% of the wavelengths emitted by a 19,000K blackbody surface are
reflected.
In total, 20% of the
reactor’s output becomes waste heat.
Since aluminium melts
at 933K, we will keep a safe temperature margin and operate at 800K. This
should have only a marginal effect on the mirror’s
reflective properties. Waste heat must be removed at this temperature. As in
the liquid fuel reactor, the coolant fluid passes through a turbine, into a
radiator and is compressed on its way back into the reactor. Neon is used for
the quartz tube, helium for the reactor walls and the gaseous lasing medium is
its own coolant.
Based on the
reference design, the reactor would have 4.56 MW/kg in output, or 3.65 MW/kg
after inefficiencies. If the radiators operate at 750K and use carbon fiber
fins, we can expect a power density for the reactor-emitter of 70.57 kW/kg.
28.9% of the
radiation emitted by a 19,000K blackbody surface, specifically wavelengths
between 120 and 190nm, is absorbed by a Xenon-Fluoride gas
laser.
They are converted into a 350nm beam with 10% efficiency in a single-pass
experiment. In our case, the lasing medium is optically thin. Much of the
radiated energy passes through un-absorbed. The mirrors on the walls recycles
those wavelengths for multiple passes, similar to the Nd:YAG design mentioned
previously. Efficiency could rise as high as the maximal 43%. This paper suggests the maximal
efficiency for converting between absorbed and emitted light is 39%. We’ll use
an in-between figure of 30%. This means that the effective power density of the
reactor-emitter-laser system is 6.12 kW/kg.
The XeF lasing medium
is mostly unaffected by temperatures of 800K, so long as the proper density is
maintained. We can therefore cool down the lasing medium with same radiators as
for the reactor-emitter (17.94 kW/kg). When we include the waste heat of the
laser, we get an overall power density of 2.9 kW/kg, after applying a 15%
penalty.
A better power
density can be obtained by having a separate radiator for each component that
absorbs waste heat (quartz tubes, lasing medium, reactor walls) so that they
operate at higher temperatures, but that would be much more complex.
Aerosol fluorescer reactor
The design can be found with all its details in this
paper.
Tiny micrometer-sized particles of fissile fuel are
surrounded in moderator and held at high temperatures. Their nuclear output, in
the form of fission fragments, escapes the micro-particles and strikes
Xenon-Fluoride or Iodine gas mixtures to create XeF* or I2* excimers. These
return to their stable state by releasing photons of a specific wavelength
through fluorescence. Their efficiency according to the following table is 19-50%.
Simply, it is an excimer laser that is pumped by fission
fragments instead of electron beams. I2* is preferred for its greater
efficiency and ability to produce 342 nm beams. Technically, this is an
indirect pumping method, but it shares most of its attributes with direct
pumping reactor lasers.
The overall design is conservatively estimated at 15 tons
overall mass, but with improvements to the micro-particle composition (such as
using plutonium or a reflective coating), it could be reduced even further. It
is able to produce 1 MJ pulses of 1 millisecond duration. With one pulse a
second, this a power density of 66 W/kg. One hundred pulses mean 6.6 kW/kg. One
thousand pulses, or quasi-continuous operation, would yield 66 kW per kg.
The only limit to the reactor-laser’s power density is heat
build-up. At 5% efficiency, there is nineteen times more waste heat than laser
power leaving the reactor. We expect that using the UV mirrors from the previous design could drastically improve this figure by recycling light that was not absorbed by the lasing medium in the first pass through. Thankfully, the 1000K temperature allows for some
pretty effective management of waste heat.
Carbon fiber panels of 1mm thickness, operating at 1000K
would handle 56.7 kW/kg. It would give the reactor a maximum power density of
2.4 kW/kg, including a 15% penalty for other equipment.
If the reactor can operate closer to the melting point of its
beryllium moderator, perhaps 1400K, then it can increase its power density to
8.3 kW/kg.
Conclusion
Reactor lasers, when
designed appropriately, allow for high powered lasers from lightweight devices.
We have multiple examples of designs, either from references or calculated,
that output several kW of laser power per kg.
The primary
limitations of many of the designs can be adjusted in ways that drastically
improve performance. The assumptions made (for instance, 1 cm thick carbon
emitter or flat panel radiators) are solely for the sake of easy comparison. It
is entirely acceptable to use 1mm thick emitting surfaces or one of the
alternate heat radiator designs mentioned in this
previous blog post.
Even better, many of the lower temperature lasers can have their waste heat
raised to a higher temperature using a heat pump. Smaller and lighter radiators
can then be used for a small penalty in overall efficiency to power the heat
pumps.
Most of the lasers
discussed have rather long wavelengths. This is not great for use in space, as
the distances the beam has to traverse are huge and it multiplies the size of
the focusing optics required. For this reason, a method of shortening the
wavelengths, perhaps using frequency doubling, is recommended. Halving the
wavelength doubles the effective range. However, there is a 20-30% efficiency
penalty for using frequency doubling. Conversely, lasers which produce short
wavelength beams have a great advantage.
The list of laser
options for each type of pumping is also by no means exhaustive. There might be
options not considered here that would allow for much greater performance… but
research on such options is very limited. For example, blackbody and LED
pumping seems to be a ‘dead’ field of research, now that diodes can produce a
single wavelength of the desired power. Up-to-date performance of those options
is therefore non-existent and so we cannot fairly compare their performance to
lasers which have been developed in their stead.
It should be pointed out that a direct comparison between
reactor and electric lasers is not the whole story. Reactor lasers can easily
be converted into dual-mode use, where 100% of their heat is used for
propulsion purposes. A spaceship with an electric laser can only a fraction of
their output in an electric rocket. For example, the 4200K laser can have a
performance close to the liquid-core rocket design it was derived from. Other,
like the aerosol fluorescer laser, can both create a beam and heat propellant
at the same time. A nuclear-electric system must choose where to send its
electrical output and must accept the 60% reduction in overall power due to the
conversion steps between heat and electricity at all times.
Finally, certain reactor lasers have hidden strength when
facing hostile forces.
Mirrors work both ways. The same optics and mirrors that
transport your laser beam from the lasing medium out into space and to an enemy
target can be exploited by an enemy to get their beam to travel down the optics
and mirrors and reach your lasing medium.
The lasing medium, assumed to be diodes or other
semiconductor lasers, has to operate at relatively low temperatures and so it
will melt and be destroyed under the focused glare of the enemy beam.
Tactics around using lasers and counter-lasers, something
called ‘eyeball-frying
contests’ can sometimes lead to a large and powerful
warship being brought to a stalemate by a small counter-laser.
A nuclear reactor laser’s lasing medium can be hot gas or
fissioning fuel. They are pretty much immune to the extra heat from an enemy
beam. It would render them much more resistant to ‘eye-frying’ tactics.
This, and many other
strengths and consequences, become available to you if you include nuclear
reactor lasers in your science fiction.
PS: I must apologize for using many sources that can only be fully accessed through a paywall. It was a necessity when researching this topic, on which little detail is available to the public. For this same reason, illustrations had to be derived from documents I cannot directly link to, but they are all referenced in links in this post.


































































Great post
ReplyDeleteAlthough reactor lasers give high efficiency i think the added complexity and the necessity to operate the reactor at high temperature is a disadvantage. I would prefer the much simpler, lighter and economical MHD generator and diode laser.
I have few questions
1)how would fusion reactor perform as a pump source?
2)what about gas dynamic laser. We can use the reactor to heat the gas and expansion nozzle to make it lase.
Reactor lasers have lower efficiency than electrical lasers in almost all cases. They make up for it with having a simpler, more robust and more powerful designs per kg. Except for the liquid and gas core reactor designs, they operate at the same temperature as regular electric lasers powered by nuclear energy source.
DeleteA fusion reactor can produce a lot of neutrons, which can then be converted into laser light using direct volumetric or wall pumping. Or, it can act as an extremely high temperature source of X-rays, which can power a photoionization laser.
Gasdynamic lasers could have very good performance in theory, but in practice we only demonstrated 0.5% efficiency.
That's alot of detail! I had to skim through this, will try and get the meat in the next week.
ReplyDelete"Mirrors work both ways. The same optics and mirrors that transport your laser beam from the lasing medium out into space and to an enemy target can be exploited by an enemy to get their beam to travel down the optics and mirrors and reach your lasing medium."
Just one thing to check. I apologise if I missed this in the post. Are phased arrays as subject to eye-ball frying contests as traditional mirrors?
Thanks! I'd love to read your thoughts on the post.
DeletePhased arrays are basically a grid of exposed laser generators. In this example (https://www.researchgate.net/publication/289793862_Optical_Modeling_for_a_Laser_Phased-Array_Directed_Energy_System), they're fiber lasers stacked next to each other, all under one electronic phase control.
As such, they are as weak as the weakest element in their construction. Generally, this will be the lowest melting temperature component. Unlike a mirror, which could survive operation at several hundred °C, a phased array would start seeing electronic components fail at 100°C.
My understanding is that it is rather easy to get a beam to heat up non-reflective, low heat capacity surfaces up to 100°C in the vacuum of space using moderately intense beams.
Drat! I read on rocketpunk somewhere that phase arrays were easier to armour than mirrors. Oops
DeleteThank you for this thought-provoking and thorough analysis. I really enjoyed it. I don't have the expertise to offer much commentary of my own, but I will definitely be referring back to this the next time I'm thinking about space laser systems.
ReplyDeleteAs a small suggestion, have you considered using something like MathJax https://www.mathjax.org for presenting equations? I understand if it's not convenient for you, but I just bring it up because something like
PD = (PDr * OE) / (1 + PDr (Ex/PDx + Ex*El/PDl + (1 - Ex*El)/PDh))
would be much easier to read with proper formatting instead of nested parentheses.
Thank you!
DeleteThe formatting of the equation is for the sake of compatibility with different forums, and it can be copy/pasted as text instead of an image.
Excellent work!
ReplyDeleteAll in all, the UF6 gas laser caught my eye. The others are just too inefficient or complex to bother. Thermal components add mass, semiconductors just die in radiation, etc.
UF4 could be a good candidate, too. Boils at 1690K.
Thanks! It took a lot of work...
DeleteSadly, the UF6 laser still hasn't been demonstrated to work so it is more on the 'plausible' side of things.
I think this Reactor-laser will be good choice for little thermonuclear
ReplyDeletedrones. Can we build 'interceptor'?
"However, Helium-3 converts neutrons into charged particles with very low efficiency, with volumetric pumping experiments reporting 0.1 to 1% efficiency overall. This is because the charged particles being created contain only a small portion of the energy the Helium-3 initially receives."
ReplyDeleteI don't understand this comment. In the (n,p) reaction on 3He, doesn't 100% of the energy end up in the charged particles? Or do you mean the neutron has already lost most of its energy to a moderator before being captured by 3He, or possibly that fission only puts 3% of its energy into neutrons?
Oh! This isn't referring to a fusion reaction, but the process where Helium-3 in the lasing gas absorbs the kinetic energy of a neutron, then turns into a fast moving charged particle that can excite the release of photons by itself. The neutrons are created by a FISSION reaction in the walls of the reactor-laser.
DeleteThis is fascinating information on how nuclear reactor lasers could be more efficient than conventional ones.
ReplyDeleteWhere can I read up about nuclear laser driven propulsion? Is there any way to heat up the propulsion gas (presumably hydrogen) hot enough that we have isp higher than ion propulsion drives? I'm guessing the container and the nozzle would be the bigger problem here. Nuclear lightbulb gives the idea of doping the hydrogen with something else.
ReplyDeleteThere are plenty of papers on electric thruster designs where the exhaust is a plasma heated by an onboard laser.
DeleteIf lasers can superheat fusion fuel to tens of millions of Kelvin, then they could also superheat regular propellant and achieve Isp on the order of 100,000s and beyond.
Of course, the penalty to doing that is extremely low thrust even with a powerful reactor, and your overall power density is limited anyway.