What we need instead is a Fusion Highway to connect the Solar System in unprecedented ways.
The art above is by GrahamTG. It depicts a Bussard Ramjet, which is relevant as all the same components (collection scoop, reaction chamber, magnetic nozzle) are necessary for the Fusion Highway to work, but are used in slightly different ways.
The ideal rocket
 |
| In Star Trek, propulsion is never a problem unless the plot demands it. |
If you had to imagine the perfect rocket, what features would it have? Solving the troubles we have with our existing chemical-fuelled engines can serve as a starting point. Limited specific impulse, limited thrust, great complexity and high cost are standard features of today’s rockets.
Logically, a perfect rocket would have maximal propellant efficiency, incredible thrust, minimal complexity and cost… or how about no propellant at all? The perfect rocket takes us up to relativistic speeds, but is also lightweight and accelerates quickly. It is instantly available and safe to use.
Only a few propulsion systems have approached this ‘ideal’ status. A Bussard Ramjet, as initially conceived, would need no propellant except what it could gather from the interstellar medium, and it could accelerate all the way up to the speed of light and back.
 |
| Relativistic ramjet. |
As we know today, it didn’t really work as advertised. An antimatter beam rocket promises amazing performance with great thrust and efficiency, but fails with regards to cost and safety. Fission fragment propulsion attempts to provide similar efficiency and uses a much safer fuel, but it lacks thrust and no-one would call it a perfect rocket.
There is another type of candidate for ‘perfect rocket’ status. Externally propelled ‘beamrider’ rockets leave the power and propellant at home and receive instead a beam that they only have to convert into thrust. Laser-driven sails are the most famous example of this approach. Powerful generators produce a laser beam that gets focused by a huge mirror so that it can concentrate its output onto very distant targets. That target, a spaceship, only has to reflect the laser beam to accelerate towards its desired direction of travel.
 |
| A kinetic mass-beam rider and its magnetic nozzle. |
Kinetic mass-beam propulsion creates a stream of high velocity projectiles that the target can deflect magnetically. However, you would need a very expensive beaming installation or very long accelerator to make these beamrider concepts practical.
We will be focusing on another external propulsion system that has many advantages over laser sails and kinetic streams. The ‘beam’ is a trail of fusion fuel pellets that is simply pre-positioned ahead of a spaceship so that it can ‘ride’ it with no additional power input of its own, up to relativistic speeds.
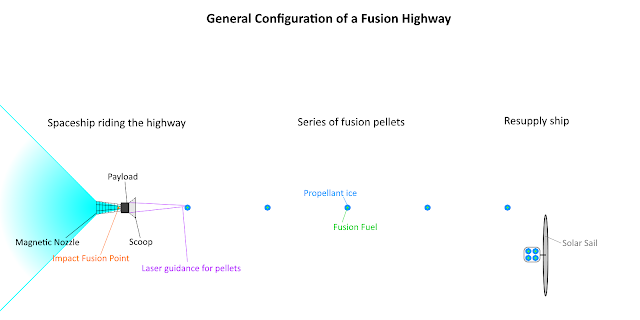
Fusion Highways
There are three elements to a Fusion Highway:
-A ‘road-laying’ system that moves pellets into position
-A series of fusion fuel pellets that align into a ‘road’
-A spaceship that ‘rides’ the ‘road’ by igniting the pellets as they pass into a reaction chamber.
There are many ways to position pellets in space. There will be very many of them in number, so a positioning method that is very inexpensive would be preferred.
The ‘pellets’ are not necessarily dumb masses of frozen fusion fuel. At the very least, they are coated in insulation and devices that report its position (like a corner reflector or low power transmitter). If they are not placed immediately ahead of the spaceship, they would need a method for correcting their position in the long term.
The spaceship itself is very simple. It has an opening that guides the pellets into its reaction chamber, using magnets or laser pulses to make last-second adjustments.
 |
| Specially shaped targets. |
The reaction chamber holds a specially shaped target mass. Ignition itself is the result of the high velocity impact between the fusion fuel pellet and the target mass. ‘Impact fusion’ can take place at velocities as low as 100 km/s, if we are able to convert the linear force from the impact into a more efficient 2D or even 3D compression.
The result is an expanding volume of energetic plasma. It bounces off the fields generated inside a magnetic nozzle so that energy is converted into thrust, and so the spaceship accelerates. When the spaceship reaches the next pellet, the cycle starts again.
The main advantages of this method is that the spaceship does not need to have a heavy reactor or a complex fusion ignition system. It just drops masses in front of the pellets and harnesses the plasma with a relatively lightweight magnetic nozzle. Unlike a remote laser beam, the energy that propels the spaceship is not the result of a massive beaming installation, but derived from the fusion fuel on-the-go. None of that energy needs to be transmitted by immense focusing optics either, and it does not get harder to operate as the spaceship gets farther from its starting point.
The pellets themselves do not need to have a huge velocity, another major advantage over a concept like kinetic stream propulsion. This means you don’t need massive accelerators to bring the projectiles up to incredible velocities, with the expectation that the spaceship can achieve at least a fraction of that velocity. On the Fusion Highway, the spaceship’s velocity is mostly independent of the fuel pellets’ velocity.
These factors mean that a Fusion Highway can be affordable and have open-ended performance.
The actual performance of this propulsion system depends on several factors. They are:
- The mass ratio between pellet and target
- The impact velocity
- Fusion fuel energy content
- Average molar mass of the pellet/target mix
- Fusion burnup and use efficiency
- Nozzle thrust efficiency
Let’s go through two worked examples to demonstrate how those factors are used.
Imagine a spaceship of 1,500 tons travelling at a velocity of 300 km/s relative to a fuel pellet track. The track is composed of 1 kg pellets, composed of 500 grams of Deuterium and Tritium fusion fuel, surrounded by 500 grams of frozen hydrogen ice. It has the potential to release 170 TJ of energy.
The mass ratio between pellet and target is 0.001; this means the spaceship is dropping a 1 gram target for the 1 kg pellets to hit. The impact velocity is 300 km/s. At this velocity, the impact of 1 gram releases 45 MJ of energy, enough to ignite the fusion fuel if the appropriate techniques are used. The frozen hydrogen ice can be shaped to help direct the kinetic energy of the impact into a compressive force that ignites the fuel.
We know that the maximum potential for the fusion fuel is 170 TJ, but not all of this energy will be transferred to the spaceship. Firstly, not all the fuel will undergo fusion. The burnup percentage might be just 10%, so only 17 TJ is released. Of that energy, 20% will be in the form of X-rays and charged particles, which will be easily converted into heat by the frozen hydrogen layer. 80% will be in the form of neutrons, which escape more easily. However, hydrogen ice is an excellent neutron absorbing material, and it should be thick enough for half the neutrons to be captured and turned into heat, so the final amount of ‘usable’ fusion energy is closer to 10.2 TJ. The kinetic energy from impact adds a negligible amount.
All this energy converts the target+fuel mix into a very high temperature plasma that expands (if timed right) inside the spaceship’s magnetic nozzle. The temperature is high enough that all particles involved become fully ionized, which simplifies our calculations as we can use perfect gas laws with reasonable accuracy. We also assume that all heating is done while the target+fuel mix is solid (so at constant volume) and that the contribution of phase changes and ionization is negligible.The heat capacity of a perfect monoatomic gas at constant volume is 12470/Molar Mass, in J/kg/K. The temperature of a gas is its energy density (Joules per kilogram) divided by its heat capacity. The rate at which the gas expands is the Root Mean Square gas velocity, which is (24942 * Temperature / Molar Mass)^0.5. If we put these equations together, we find that the molar mass cancels out and therefore:
- Plasma RMS velocity = (2 * Energy Density)^0.5
In this example, 10.2 TJ of energy is distributed in 1.001 kg of matter. This gives a value for the plasma expansion velocity of 4,511 km/s.
A noteworthy consequence of molar mass and heat capacity cancelling out is that the nature of the gases expanding does not matter. In theory, we are free to use abundant propellants like water or silicate rocks instead of being restricted to bulky hydrogen, although lighter molecules absorb neutrons better and lead to greater overall efficiencies.
We must make an adjustment to this expansion velocity. The fuel pellet is initially retreating from the spaceship at 300 km/s. After impact, it loses 0.1% of its relative velocity, becoming 299.7 km/s. This must be subtracted from the expansion velocity to find the actual velocity of the plasma relative to the magnetic nozzle. That value becomes 3,198 km/s.
 |
| Fusion plasma within a magnetic nozzle. |
The performance of this propulsion system is quite spectacular. Nozzle thrust efficiency is realistically 80%, so the spaceship inputs 1 gram, and it gets 1.001 kg exiting the nozzle at 2,558 km/s. The effective exhaust velocity is multiplied by a thousand to 8.52 times the speed of light.
If there is a 300 km gap between the fuel pellets, the net propulsive power the spaceship outputs is 3.27 TW and its average acceleration is 0.17g.
Now let’s repeat these calculations for a much higher relative velocity.
The same 1,500 ton spaceship rides a track of the same 1 kg pellets, but at 90,000 km/s.
The mass ratio between pellet and target is increased to 2. The spaceship drops a 2 kg frozen hydrogen target to impact the same 1 kg fuel pellet. The total mass of the mix after impact is 3 kg, so the ‘retreating velocity’ is reduced to 30,000 km/s.
This also allows us to extract two thirds of the potential kinetic energy from the impact; 2700 TJ.
The fusion fuel is compressed by a large amount of target material at much higher velocities, so excellent burnup percentages are to be expected, up to 25%. We can hope for 42.5 TJ to be released, and all of it to be absorbed by the extra target mass we’re putting in. Total energy adds up to 2742.5 TJ.
Energy density is 2742.5 TJ over 3 kg or 914.17 TJ/kg. We can expect a plasma expansion velocity of 42,759 km/s.
You will notice that the margin between plasma expansion velocity and retreating velocity at 12,759 km/s is much slimmer than in the previous calculation. The spaceship puts in 2 kg of propellant and gets 3 kg of plasma, so its effective exhaust velocity is a bit higher at 19,138 km/s, or 15,310 km/s if we consider nozzle efficiency.
That same 300 km gap between fuel pellets means that the spaceship encounters 300 pellets per second. Net propulsive output is 105,478 TW (if the spaceship’s nozzle can survive it!) and average acceleration is 3.12g.
Velocity Bands
The performance of the Fusion Highway depends on the velocity of the spaceship relative to the fuel pellets. There are four distinct ‘velocity bands’ that significantly affect performance:
 |
| Logarithmic scale on y-axis, all units in C. Green is Fusion band, Yellow is Kinetic band, Red if Relativistic Band. |
- Sub-ignition band
The sub-ignition band of velocities is where the relative velocity of the fuel pellets and the spacecraft is insufficient to ignite fusion reactions. With dumb pellets of fusion fuel and a simple target, this can be as high as 1000 km/s. With specially shaped sphere-section imploding targets and other features that improve compression upon impact, this can be brought down to below 100 km/s. Further into the future, a few tens of km/s might be all that is needed for impact fusion thanks to hotspot ignition or the assistance of external magnetic fields.
 |
| A Fusion Highway would have multiple entry and exit ramps. |
A spaceship would have to reach this minimum velocity by some other means before it can start using the Fusion Highway. Think of it as a car accelerating along the entrance ramp to a highway.
This could be accomplished by consuming the first few fuel pellets using an onboard ignition system. The frozen fusion fuel could be compressed by magnetic fields, blasted by plasma jets or compressed by ablative laser beams… ignition of the fusion reaction would produce energy that is converted into thrust, allowing acceleration up to the impact fusion threshold velocity. It would not be an ideal solution, as the heavy fusion ignition system would not be of much use for most of the spaceship’s journey, but it would allow for free entry and exit from the Fusion Highway at any point.
A better solution could be the use of ‘boost tracks’ that have a high relative velocity to the spaceship, somewhat like a conveyor belt that the spaceship can ride until it reaches the Fusion Highway at the necessary velocity. The boost track is a series of fusion fuel pellets that are shot at the spaceship’s position at above the threshold velocity for impact fusion ignition, doing away with the need for heavy onboard propulsion or ignition systems. The spaceship can then ride this short boost track and then divert to the main Fusion Highway once it has built up enough speed.
If the threshold velocity is very low, then some alternative options become available. For example, the boost track is composed of pellets put on a retrograde orbit that the spaceship only needs to intercept at the right time. A spaceship in Low Earth Orbit would be travelling at about 7.7 km/s relative to the surface. Pellets in a retrograde orbit would be travelling at 7.7 km/s in the opposite direction, adding up to a relative velocity upon impact of 15.4 km/s. Pellets on a retrograde near-escape trajectory, perhaps falling from the Moon, could reach a peak velocity of over 11 km/s and achieve 18.7 km/s upon impact.
If these orbital velocities are too low, then interplanetary relative velocities can be used. An Earth-orbiting spaceship facing retrograde fuel pellets along the same orbital path would achieve a relative velocity of up to 7.7+29.8+29.8: 67.3 km/s.
-Fusion band
 |
| A fusion rocket at full blast, featuring liquid droplet radiators. Imagine it has a collection scoop for fuel pellets in front. |
The fusion band of velocities is where the spaceship’s velocity relative to the Fusion Highway is enough to ignite the fuel pellets by impact. There is a minimum and maximum velocity here.
The minimum velocity, as described above, is the threshold for igniting fusion reactions upon impact. The maximum velocity is more complicated.
In this band of velocities, the energy gained from each impact is dominated by the output of the fusion reaction. In the 300 km/s example that was calculated in the previous section, 99.9996% of the energy was derived from the fusion reaction. Because the same amount of energy comes from igniting the same amount of fuel, the expansion velocity of the resultant plasma is nearly constant. However, as the spaceship’s velocity on the highway increases, the retreating velocity increases.
At very low relative velocities, the difference between expansion velocity and retreating velocity is huge. Effective exhaust velocity is at its highest. At increasing relative velocities, the difference between expansion velocity and retreating velocity becomes smaller and effective exhaust velocity falls quickly. At some point, the relative velocity is nearly equal to the expansion velocity and no thrust is generated; effective exhaust velocity becomes zero. This is the limit of the fusion band.
The maximum velocity is therefore close to the expansion velocity of the ‘pure fusion’ plasma. This depends, as shown in the previous calculations, on how much energy can be extracted from the fusion fuel divided by the mass of the fuel pellet.
For example, a fuel pellet that is 50% Deuterium-Tritium fuel, has a 10% burnup ratio and is able to convert 60% of the fusion energy into heat would manage an energy density of 10.2 TJ/kg, and create a plasma that expands at 4516 km/s. The maximum velocity in the fusion band using this pellet will be around 4516 km/s.
A better pellet helps extend the fusion band of velocities. Deuterium and Helium 3 release nearly 95% of their output in a form that can be converted into heat. Advanced compression and confinement techniques can improve burnup to perhaps 25%. If the fuel pellets can be made entirely of DHe3 fuel, we could manage an energy density of 83 TJ/kg and therefore have a plasma that expands at 12,950 km/s.
It is important to extend the fusion band of velocities to be as wide as possible as this is where the outrageous effective exhaust velocities are possible, multiple times the speed of light in many cases. The spaceship only needs to drop the smallest target masses to ignite the fusion reaction, and can then ramp its speed up and down easily.
-Kinetic band
 |
| A RAIR spaceship. |
After the fusion band’s maximum velocity is crossed, there comes a point where tiny target masses are no longer possible. The target/fuel mix must have a retreating velocity lower than the plasma expansion velocity. Calculations show that this requires a target to fuel pellet mass ratio of over 2, i.e. 2 kg of target mass to catch 1 kg fuel pellets.
The kinetic energy added upon impact quickly becomes dominant. In the 90,000 km/s example above, the kinetic energy from the impact represents 98.45% of all the energy that the plasma gains. The fusion fuel in the pellets can actually be replaced with inert material and we won’t see a significant drop in performance (and this will really help keep the overall costs low!).
There is an optimal mass ratio between the target and the fuel pellets that provides the best effective exhaust velocity at any impact velocity. Since the fusion output provides only a small fraction of the energy gained from impact, this optimal mass ratio depends mostly on the performance of the magnetic nozzle and less on the composition of the fuel pellets.
Furthermore, as the impact velocities increase, retreating velocity increases linearly (it is a momentum transfer) but the kinetic energy added to the expanding plasma increases quadratically. Calculations show that effective exhaust velocity improves gradually at higher velocities. A spaceship can ride the Fusion Highway more efficiently the faster it goes.
However, the great reduction in effective exhaust velocity and the extreme velocities involved make this unsuited for interplanetary travel. Also, in this band of velocities, a spaceship travelling along Fusion Highway acts very much like a Ram-Augmented Bussard Ramjet.
-Relativistic band
After a while, relativistic effects come into play. The equations we’ve used to estimate the performance of this propulsion system tell us that a spaceship can ride a Fusion Highway up to large fractions of the speed of light with only moderate amounts of target masses. However, some assumptions start to break down.
For example, we assume that the collision between the target mass and the fuel pellet is elastic, that the kinetic energy is fully absorbed and converted into heat, and that the fusion reaction has time to ignite and spread its energy throughout the mix before it all expands outwards.
Some of these things won’t hold up at relativistic velocities. The fuel pellet will start to act instead as penetrating radiation that digs through the target masses. The plasma might expand too quickly for the fusion reaction to transfer its energy efficiently, or it might reach temperatures so great that there is significant energy loss through blackbody radiation before it fully expands.
When do these relativistic effects come into play? It is hard to say. 30% to 50% of the speed of light seems like a plausible limit. At 0.5C, the Lorentz factor is only 1.15, but hydrogen acts as 145 MeV radiation and the plasma temperature is supposedly in the hundreds of billions of Kelvin.
This is not to say that a Fusion Highway can’t be used beyond 0.5C, but that a much more complicated analysis is required to determine how its performance is affected. What we can conclude for now is that attempting to extend a Fusion Highway beyond the Solar System, to enable interstellar voyages, is a topic that needs its own separate treatment.
Interplanetary Design
Let’s go through two complete Fusion Highway designs for use in interplanetary travel. One is modest and uses conservative assumptions, the other is more futuristic and fully illustrates the awesome potential of this propulsion method. You will note that we do not go beyond velocities within the fusion band.
-Modest example
For the modest example, we will use 0.5 kg fuel pellets that are 10% Deuterium, surrounded by 90% water ice. Deuterium is abundant throughout the Solar System and provides about 80 TJ/kg of fusion energy. Fusion burnup will be about 10% and the usable fraction of that energy is 70%; the expected energy density is about 560 GJ/kg.
An interplanetary transport system will consume a lot of fusion fuel and propellant, so it would appreciate getting to use cheaper options. Deuterium is a relatively abundant fusion fuel and it can be extracted from water anywhere in the Solar System.
 |
| This could be a solar sail carrying deuterium off a comet resupply station. |
Each fuel pellet is covered in multiple layers of very thin reflective aluminium sheets, which serve as thermal insulation from sunlight, as well as a ‘harness’ made of plastic wires. That harness allows for clusters of pellets held inside a payload bay, and attached to large solar sails.
These sails depart from Earth and dive down towards the Sun. A close pass allows for great acceleration and a trajectory that shoots back up to Earth with a relative velocity of about 100 km/s. They then drop the fuel pellets in a line, forming a boost track.
Each solar sail can position these boost tracks with only a few months’ notice. It is more practical to send off multitudes of these sails, to create regular opportunities for travel, perhaps every week. After dropping off their payload, the solar sails can adjust their outwards trajectory to encounter a gas giant planet for a gravity assist back into the Solar System, and as they are dozens of times lighter than before, they can very slowly cancel out their velocity and return to Earth.
The Fusion Highway itself is a 35 million km long track of fuel extending away from Earth, consisting of around 12 thousand fuel pellets.
They are positioned in sections of perhaps 100 pellets by solar statites, which are solar sails large enough and lightweight enough to counter the Sun’s gravity and hold a position in interplanetary space indefinitely. Another 35 million km long segment leads up to the destination.
The spaceship is a 711 ton vessel. It carries a 100 ton payload and 11 tons of target masses. 500 tons are dedicated to the propulsion system, including a magnetic nozzle that is only 50% efficient at converting the expanding plasma into thrust.
 |
| Small spacecraft performing rapid trips to the Outer Planets and back. |
We set the power density of the propulsion system to 2 MW/kg (totalling 1 TW), which might seem excessive, but note that this is only a magnetic nozzle and very high temperature radiators, nothing else. It must not be compared directly with typical fusion rockets, who have to use heavy ignition equipment, power recovery cycles and lower temperature radiators. The remaining 100 tons consists of shielding, electrical equipment and comfortable living spaces.
As mentioned before, the performance of the Fusion Highway depends on the velocity you ride it at. In the table below, we can see that the deuterium releases 280 GJ of useful energy, allowing for a plasma expansion velocity that is a rather constant 1058 km/s. The initial effective exhaust velocity is an impressive 479,420 km/s, dropping to 79,800 km/s at a relative velocity of 900 km/s.
Here’s the performance table:
Repeating the calculations for every 50 km/s increase in relative velocity allows us to calculate the necessary mass ratio required to accelerate across each 50 km/s step. To accelerate from 100 km/s to 150 km/s, the spaceship needs to expend about 147 kg of target masses. For the final 850 km/s to 900 km/s, it expends about 890 kg. The cumulative mass ratio for accelerating all the way from 100 km/s to 900 km/s involves multiplying the mass ratios of each step, for a final value of 1.008, or about 5.6 tons on top of the spaceship’s 700 ton dry mass.
Here’s a table of mass flow, acceleration and displacement parameters for a spaceship limited to 1 TW riding this modest Fusion Highway:
Acceleration increases over time because the exhaust velocity of the plasma decreases the faster the spaceship goes. For the same propulsive power, lower exhaust velocity translates into higher thrust.
Because each 0.5 gram of target mass is matched with 0.5 kg of fuel pellets, we can say that accelerating up from 100 km/s to 900 km/s requires 5600 tons of fuel pellets. That’s 560 tons of deuterium and 5040 tons of frozen water. To slow down back to 100 km/s and with an additional margin on top, we used a mass ratio of 1.016, or about 11 tons of target masses.
What sort of performance do we get out of this set-up?
The spaceship has an initial acceleration of 0.6g. It takes 23.2 hours to complete its acceleration, with a peak acceleration at the final pellet of about 3.6g. It will cruise at 900 km/s, enough to get it from Earth to Jupiter in 10 days, or from Venus to Neptune in 2 months.
As an interplanetary transport system, it does not require very advanced technology or huge amounts of rare fuels. It is rather easy to replenish the bulk of the fuel pellet material, and while the 35 million kilometre long tracks might seem excessive, they are only constellations of a few hundred satellites holding positions in interplanetary space. Today’s mega-constellations are far more complex!
Replenishing thousands of tons of water and hundreds of tons of deuterium would be the bigger challenge, but there are a few months to accomplish that task while the boost track solar sails make their trip around the Sun.
-Futuristic version
For this second example, we use more optimistic assumptions and have no care for costs.
We will use 10 kg fuel pellets that are 0.5% Deuterium and 0.5% Helium-3, surrounded by 99% frozen hydrogen. Burnup will be 25%, and the usable energy fraction is 95%, so each pellet is expected to release 8.38 TJ. We are smothering the fusion fuel in inert mass so that average energy density and therefore exhaust velocity is reduced, in favor of increasing thrust and acceleration.
 |
| A large SDI-era railgun meant to shoot masses at many km/s. |
In the future, waiting around for months so that a booster track is ready might be inacceptable, as there will be a need for trips to be completed upon short notice. So, instead of propellant-free and very cheap solar sails, we use coilguns to shoot out a boost track. The coilguns will only need to achieve velocities of only a few km/s, but this will be sufficient (and energy/infrastructure costs remain low).
The boost track will consist of fusion fuel pellets encapsulated in fissile material, such as Plutonium 239. Fission reactions can be ignited by high velocity impacts, and at much lower velocities than fusion reactions. A fission-fusion hybrid booster track will be very expensive, but it would mean that a spaceship can start impact ignition from an initial velocity of less than 1 km/s!
Each fission-fusion pellet consists of 2 kg of Plutonium surrounding the 10 kg fusion fuel/hydrogen mix described above. They are struck by 1 kg frozen hydrogen target masses at multiple km/s. Average energy density after impact is 12.95 TJ/kg, so the plasma expands at 7090 km/s. The penalty from the retreating velocity is negligible. Effective exhaust velocity (1kg in, 13kg out at 80% efficiency) is 942,170 km/s. A mass ratio of just 1.004 is needed to accelerate from 0 to 200 km/s. The boost track would be about 3.6 million km long. The spaceship would accelerate at about 0.67g along this track and exit after 8.9 hours.The spaceship then switches from the booster track to the main Fusion Highway. It is going faster than what is strictly necessary to ignite an advanced fusion fuel pellet upon impact, but it will help enable the following setup:
The Fusion Highway will consist of several lanes.
The ‘high speed lane’ is composed of many 10kg fusion fuel pellets, intended to be consumed by large spacecraft trying to get to places quickly. Parallel to this are ‘service lanes’ that propel smaller ‘tender’ craft that replenish the high speed lane. A tender craft has its own magnetic nozzle and is loaded with fuel pellets. It accelerates up a service lane to 100 km/s, and then drops off the fuel pellets to replenish the high speed lane. This causes the high speed lane’s pellets to move outwards at 100 km/s.
Since the spaceship coming off the booster track is travelling at 200 km/s, it can catch up to the moving high speed lane pellets at 100 km/s.
Why have a moving lane? The Fusion Highway will have to be millions of kilometres long. Having tender craft travelling at 100 km/s means that its entire length can be replenished quickly. For example, a 1000 km/s Fusion Highway is 69 million km long, and the tender craft can get it ready for the next trip in about 8 days. A 5000 km/s Fusion Highway will be 495 million km long and be ready every 57 days. Even faster tender craft, and a longer booster track to catch up with them, would be necessary for the longest Fusion Highways.
The tender craft can also correct the positions of the pellets that they have dropped on their return journey back up the service lane. Frequent resupply flights can provide near continuous adjustments to pellet positions.
The spaceship we’ll use carries a 100 ton payload. It has a 1000 ton propulsion system that is 80% efficient and can handle 10 TW in the exhaust plasma. 100 tons are dedicated to other equipment, and 7.6 tons to target masses, adding up to a total mass upon departure of 1207.6 tons.
The spaceship can choose to exit the Fusion Highway once it has achieved its desired velocity. This can range from 100 km/s to 12,000 km/s (in addition to the 100 km/s granted by the boost track). It has enough target masses to reach the maximum velocity listed in the table below, and slow back down again.
Acceleration on the Fusion Highway starts off at 2.7g, peaking at 23.5g at the highest velocities. It is likely that pellets start getting skipped to reduce acceleration if there is a human crew onboard.
If a middling velocity of 2000 km/s is deemed sufficient, then the spaceship needs to ride the Fusion Highway for 27.2 hours. The acceleration length is 148 million km. Departing from Earth, the spaceship can reach Saturn in just 7.4 days. The spaceship expends 704 kg of target masses altogether, matched by 7040 tons from both acceleration and braking tracks.
Closer destinations are limited by the length of the Fusion Highway. A continuous line of pellets from Earth to Mars, if both planets are on the same side of the Sun, may span as little as 55 million km. In this case, we can treat the spaceship as a classical Torchship that maintains a constant acceleration and perform a Brachistochrone trajectory: accelerate up the mid-point and then slow down to a stop. With 2.7g of acceleration, such a short trip can be completed in 25 hours.
But what if we want to blaze a trail across the Solar System at 12,000 km/s? The spaceship would need to spend 3 days on either end of the track, and the acceleration length becomes 8.34 AU long, so the minimum trip distance is 16.68 AU. One possible use for such a velocity is crossing from Saturn to Neptune if they were on opposite sides of the Sun… a 39.6 AU trip which could be completed in a mere 9.4 days from stop to stop.
A total of 7.6 tons of target masses would be expended on the system-spanning dash, matched by 76,000 tons of fuel pellets, of which 380 tons is rare Helium 3. That would make it a pretty expensive endeavour for delivering just 100 tons of payload.
Comparison with alternatives
These performance figures stand out even more if we try to recreate them using alternative propulsion systems. Let’s work out how large a fusion rocket we would need, starting with the modest Fusion Highway example.
Normally, fusion propulsion can manage to produce the same exhaust velocity as the expanding plasma within a Fusion Highway rider's magnetic nozzle. A deuterium-burning rocket would have a maximum exhaust velocity of 12,900 km/s or 4.3% of the speed of light (it’s the average velocity of the reaction products from a ‘naked’ reaction), so normally accelerating up to 900 km/s and back down again is no problem.
However, needing to have an electricity generating loop and fusion ignition equipment would bring down the average power density of a realistic fusion rocket down to 300 kW/kg at best. The maximum average acceleration of a 300 kW/kg fusion rocket that aims to achieve 1800 km/s of deltaV is about 0.02g.
This limit exists even if we increase the power of the propulsion system to 10 TW or even 100 TW. At this acceleration, it would take 53 days to reach the desired 900 km/s transit velocity, which is clearly insufficient.
If we want the same trip times, acceleration must average 1.1g, which means that power density must be increased massively. This becomes unfair to the assumption made for magnetic nozzle the Fusion Highway rider uses...
 |
| The traditional fusion-propelled spaceship will struggle to match a Fusion Highway rider's performance, and start to look like Project Daedalus-inspired designs. |
The futuristic Fusion Highway is even harder to match.
To perform a 12,000 km/s dash, a total deltaV of 24,000 km/s is required. A ‘naked’ Deuterium-Helium3 fusion reaction manages an exhaust velocity of 26,700 km/s or 8.9% of the speed of light, therefore we would need a mass ratio of 2.45.
If we insist on recreating the 4.63g average acceleration while having the propulsion system representing 99.9% of overall dry mass, then the fusion rocket would need a minimum power density of 2.1 GW/kg. It would deliver 420,480 TW of fusion power. If we add 100 tons of payload and 100 tons of other equipment, we get a 200,000 ton dry mass and a 490,000 ton wet mass. About 145,000 tons of rare Helium 3 would be needed to deliver the 100 ton payload, despite the unfair power density advantage this super-advanced fusion rocket has over the already futuristic magnetic nozzle of the Fusion Highway rider.
Now let’s compare the Fusion Highway to the Laser Beamrider.
We start with the modest Fusion Highway. Achieving the 1800 km/s deltaV is no problem for a laser-propelled sailcraft. Acceleration is instead the main challenge.
A laser perfectly reflected by a mirror delivers 1 Newton per 150 MW. Accelerating at 1.1 g means that each kilogram of onboard mass is matched by 1.62 GW of beam power. But how much beam power can a sail really handle?
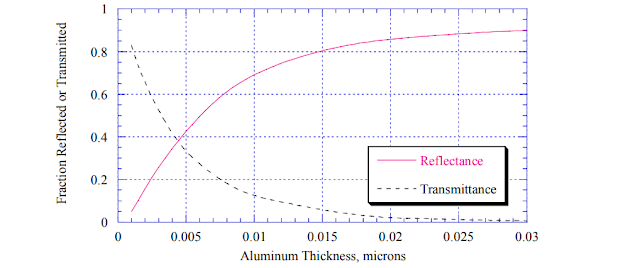 |
| Zubrin's ultra-thin aluminium sail. |
A simple solid aluminium sail, even with 90% reflectivity, can only survive a beam intensity of 86.8 kW/m^2 and if reduced to 30 nanometres thickness, the minimum thickness needed to achieve such a reflectivity, it would have an area mass of 81 milligrams per square meter, giving us a propulsion system with a power density of 1.07 GW/kg. It would provide an acceleration of only 0.36g, without payload.
To accelerate at 1.1g, a very advanced laser sail design will be required. Jordin Kare proposes dielectric laser sails that can survive much higher beam intensities, but require nanoscale engineering across kilometres-wide surfaces.
In one example provided, a sapphire sail that is 57 nanometres thick and able to operate at 1563 K can handle 34 MW/m^2 but only masses 226 milligrams per square meter. Alone, it can accelerate at 100g. Or put another way, 1 kg of this sail material can accelerate 89.9 kg of payload at 1.1g.
100 tons of payload and 100 tons of other equipment could be attached to 2.22 tons of sapphire laser sail. The sail would have a diameter of 3.56 km and receives 327.3 TW of beam power. It will be difficult to keep such a gigantic structure from collapsing under 1.1g acceleration.
Solid state lasers would have an efficiency of about 60%, so the electrical input required to generate such a beam is a whopping 545 TW. That’s over 250 times more than the world’s entire electrical output today. A beam generator station would be needed at both departure and arrival ends of the spaceship’s trip, or something like a Laser Web is needed to relay the beam across interplanetary distances. It might be expensive.
We can now try to estimate the laser sail performance needed to match the futuristic version of Fusion Highway.
Acceleration rises to 4.63g on average. The 200 tons of payload and other equipment must sit at the center of a 7.22 km wide sapphire sail that masses 9.26 tons. It receives 1,425 TW of beam power, requiring perhaps 2,375 TW of electrical power...
Consequences
A Fusion Highway has some clear advantages over other methods of rapid interplanetary travel. It might not be as flexible as a rocket engine or as versatile as a beamed propulsion system, but it allows small, lightweight spacecraft to reach very high velocities with minimal use of expensive fuels or complex equipment.
 |
| What multiple Fusion Highways waiting to be used might look like. |
It does require time to set up and replenish, but as described in the multi-lane futuristic example, the Fusion Highway can be used to replenish itself. Multiple departures in quick succession might have to be served by multiple Fusion Highways aimed in the same direction, while multiple travel windows would require Fusion Highways spaced radially along a departure point’s orbital path. These requirements suggest that busy travel routes would end up having many interconnected Highways, making the ‘road network’ analogy valid.
Furthermore, it creates the possibility that small waystations in interplanetary space would have a useful role. A comet full of water and deuterium could replenish routes bringing spaceship to it, and since so little target masses are needed for a spaceship to ride a Fusion Highway, the opportunity cost for using them to visit different destinations is low. This could result in chains of smaller bodies, from moons to asteroids, that can be visited one after the other at low cost to the spaceship. It might be entirely possible to have ‘road trips’ with many stops in space, which would be interesting to scifi authors.
Another interesting consequence is that the consumption of large quantities of water and the deuterium it contains would favor the occupation of icy moons and outer Solar System bodies. Interplanetary colonization tends to neglect these sites for their poverty in terms of metals, minerals and solar power. With Fusion Highways, they instead become abundant sources of fusion fuel that are easier to keep connected to a wider interplanetary network of Highways than a dry inner Solar System body like a metallic asteroid.
Different users will demand different types of Fusion Highways. The bulk of transportation would be done with the cheapest ices and fusion fuels, which is why we often mention water and deuterium, but there is a performance edge to be gained from using Helium 3 fuels. Some spaceships will have smaller magnetic nozzles that cannot handle as much fusion power, while others will want to maximize acceleration. This suggests that there might be Fusion Highways with small, infrequent pellets, other faster tracks with large, frequent pellets, and even military routes held in reserve that have the highest quality fuels.
 |
| Uranus and its moons might become an attractive destination. |
Finally, it is important to consider that Fusion Highways won’t operate alone. They are best served in combination with other propulsion systems, whether it is solar sails that resupply the Highways or independent rockets that can complete the ‘last mile’ of a delivery. It creates the possibility that the typical interplanetary spaceship is actually a multi-modal craft, which uses many propulsion systems that complement each other. For example, a magnetic nozzle and a few target masses are not a major burden to a fusion-propelled spaceship that can also deploy lightweight sails to ride a laser beam.












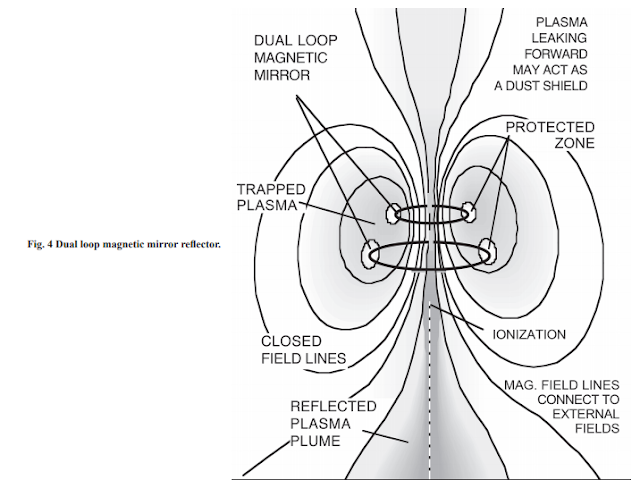
I'm a bit confused on how the spacecraft slows down using the highway. Is there a fusion off-ramp?
ReplyDeleteIf the fuel pellets are entering though a hole in the front of the ship, hitting the impactor and igniting, before being exhausted out the back, how do you pull off a brachistochrone? To slow down the acceleration needs to be opposite to the direction of the incoming pellets. Maybe have the fuel pellets be able to enter both ends of the ship and have magnetic nozzles on both ends. That method might break the highway though when decelerating since the exhaust could deflect incoming pellets.
The highway does seem really good for achieving high velocities though; perfect for interstellar travel since you could use a magsail at the destination to bleed off speed.
Yes, there will be another Fusion Highway at the destination to slow down.
DeleteThe spaceship can work in reverse. The fusion nozzle would act as the scoop, directing a fusion fuel pellet to hit a target near its throat. The expanding plasma then bounces off the magnetic fields and exits the nozzle ahead of the spaceship. Except, the relative velocity between the spaceship and the target+fuel mix is ADDED to the exhaust velocity instead of SUBTRACTED.
I would not worry about the exhaust disturbing fuel pellets ahead of the spaceship during braking. The exhaust gases travel very quickly in all directions and therefore become very spread out. For example, 1kg of plasma expanding at 10,000 km/s would have a density of about 2.38*10^-13 kg/m^3 after a millisecond. This is similar to the density of our atmosphere at an altitude of 600 km. As you know, drag is not a big problem over these short timescales at these altitudes, as demonstrated by the ISS orbiting at 400km.
I do think some extra work is needed for interstellar travel. A Fusion Highway alone can get you to 4-5% of the speed of light using only the fusion band of velocities, perhaps up to 20% if you use the kinetic band and a whole lot more propellant. That's still 21 years to the closest star!
Super interesting as usual thanks! I was wondering if the "highway pellet dispensers" could possibly be placed on resonant orbital patterns so as to create the acceleration lanes. In the same way of galactic arms for instance 🤔
ReplyDeleteThank you!
DeleteThat's a smart idea. It permits a single launcher to create a whole network of Fusion Highways that are made available for travel at regular intervals.
The difficulty is in the fact that the Fusion Highway will want to follow a very straight trajectory, while these orbiting pellets will instead curve around to form closed orbits. If you try to increase the size of the orbits so that they look somewhat straight all the way out to Jupiter, you'll find that the pellets have to be launched at beyond solar escape velocity...
"If you try to increase the size of the orbits so that they look somewhat straight all the way out to Jupiter, you'll find that the pellets have to be launched at beyond solar escape velocity..."
DeleteIf do solar escape from Venus distance and when it crosses Jupiter distance, it will have gone a shorter distance then a solar escape from Earth when it crosses Jupiter distance. But this is in regards to a hohmann solar escape trajectory.
And if doing hohmann solar escape from close to sun {say within 10 radius of Sun, it will go "straighter" to Jupiter distance as from Venus hohmann solar trajectory.
But from close to Sun hohmann escape, if add say 100 km/sec [or 1000 km/sec} above the needed hohmann escape velocity, it doesn't seems make "much" straighter distance to Jupiter distance.
It seems when doing interstellar one using Sun and/or Jupiter {or Saturn} and not really doing hohmann transfer, but it seems to me that hohmann transfer near the sun is about as straight as it gets.
I believe that once a Fusion Highway is in place, it becomes easy to install heavy equipment at the destination. This can in turn be used to make Fusion Highways even more effective and efficient.
DeleteFor example, you can install a fuel pellet recovery system near the destination. It can take the form of a laser beam acting of small sails attached to the pellets, or a spaceship that goes and physically collects the pellets before they leave the Solar System.
Then it all makes a lot more sense to me now. If there are terminals at the end of each highway that collect unused pellets and launch them in a different direction (or back where they came from), the whole system seems a lot more efficient when using such straight-line trajectories. You could (and should) even reclaim some of the kinetic energy that was used to launch the pellets in the first place.
DeleteThe whole time I was reading the blog post I was thinking that if the pellets are following a specific ballistic trajectory, the spaceship would leave that trajectory as it was accelerating due to the pellets. However, if there is an approximately straight path from one terminal to the next, it does seem like it could work as you would only need minute adjustments to stay on the trajectory.
The only detail left that I wonder about is "how straight?" For example, the pellets would certainly have to exceed the escape velocity of the Sun, which is ~16.6 km/s. However, even near this velocity, their trajectory would be very curved from the reference frame of any two bodies, so each pellet would likely have to travel many times this velocity to minimize inefficiency from trajectory adjustments in the ship.
For example if the pellets are travelling at, say, 100 km/s from the reference frames of the two terminals, a formidable but not insurmountable velocity, then the ship using the highway would need to travel in excess of 200 km/s in the same reference fram, which is very much achievable even for fission drives. The question is, is the initial speed enough such that the trajectory of the pellets is minimally perturbed, allowing the ship to travel at thousands of km/s between the two terminals without having to thrust too far towards the normal/radial direction?
Consider this:
DeleteSolar gravity beyond the Asteroid Belt is less than 1 mm/s^2 or 0.1 milligee. If you drop something with no orbital velocity, let's say from a statite, it will 'fall' by 0.5 mm after 1 second, 5 cm after 10 seconds and 1.8 meters after 1 minute.
This means that if you drop your fusion pellets just a short time before the spaceship riding the Fusion Highway arrives, you can guarantee that they will be intercepted in the right location.
Also, you can use more advanced techniques to gain even more control over the pellets over that short period. If they are charged, you can manipulate them with electromagnetic fields or electron beams from a distance. Or you could use light pressure from a laser to gently push them back into position.
This is a very interesting idea - even in a blog full of interesting ideas!
ReplyDeleteI'm wondering about simplification using your multi mode idea - rather than using fission powered "acceleration lanes, simply have the pellet launcher and ship's magnetic field operate together during acceleration as a kinetic beam rider. Once up to speed, the mass driver shuts down while the spacecraft reorients the magnetic field to direct the fusion plasma, while the opening at the front simply scoops up the pre placed pellets (which were delivered ahead of time by the launching mass driver)
The fusion engine can be used to decelerate, and any final course corrections can be done reconfiguring the ship as a beam rider once again.
Thanks.
DeleteMy objective was to really lean on the 'no huge generator/launcher/mass driver' aspect but it is entirely possible to combine them with a Fusion Highway.
Perhaps even more interesting is using kinetic energy from falling masses for propulsion, as in the Interplanetary Kinetic Energy Exchange scheme.
@ Matter Beam: Once again, very impressed!
ReplyDeleteI say this respectfully: I think of the Fusion Highways as a sort of "Pac Man in S-P-A-A-C-E!"
Does this concept obsolesce or complement macrons?
Thanks, Again
I appreciate the compliment.
DeleteI think this concept doesn't interact much with macrons. Fuel pellets are large and relatively slow, while macrons are very small and very fast. If you try to use macrons for a Fusion Highway, you'll raise the 'ignition velocity' threshold to very impractical values.
You're welcome, MB. So would:
Delete1) macron tech be used in some circumstances while FH in others?
2) one technology be quicker to develop than the other?
3) one technology be technically "superior" to the other (and under what circumstances)?
You've given thoughtful, comprehensive, and detailed descriptions of several different
means of space transportation (propulsive an otherwise)- a "surfeit of riches".
I'm trying to grasp about where and how these space transportation means might best be used, when they might be developed, and what might supersede them.
Macrons are most useful for their high velocity. This is great for using them as weapons, or for transmitting momentum/energy across really huge distances quickly.
DeleteA fusion highway doesn't really use those advantages. The method for laying out a track can be as slow as you like. The fuel pellets themselves are too big to be accelerated using the methods used in a macron gun.
I think they will have very different development paths, and even when both are fully mature technologies, they will see different uses.
For example, a laser beam relay network established between Mercury, Venus and Earth could support Fusion Highways between them, if each pellet cluster rides on laser sails in short orbits. Then at the same time, you might have macron beaming stations used to move around asteroids in the Outer Solar System, because the distances are just too huge and waiting around the Fusion Highways to get into position takes too long.
Well that paper is from 1979, well before US had serious ICF projects. NIF is consistently imploding at 300km/s to no avail.
ReplyDeleteI believe the reason why NIF is not succeeding is because they do not sufficiently fulfil the Lawson criterion. For inertial confinement, you can either increase confinement time or the particle density of the confined fuel.
DeleteHere, in M.B.'s scheme, the increased mass to area ratio of contact between collapsing fuel elements, helps provide more compression, increasing local number density. The increased mass also provides additional confinement time, by keeping the fuel together for longer, through its sheer inertia.
NIF might be able to go way higher than just the "scientific" breakeven, if they had a bigger fuel pellet to compress, and a waaaaaay bigger laser, to compress it with, at the same 300km/s.
There are other factors too.
DeleteThe fusion pellets here are about a million times bigger than the small targets used in experiments today. Having such a large scale really helps with ignition.
Kinetic compression is also much more efficient than laser compression, by a factor 100x at least.
And finally, the energy available from these impacts is huge. Dozens of megajoules, all delivered in microseconds. No laser today can match that!
Hi, Matterbeam.
ReplyDeleteLong time reader, first time caller. It's actually my art -- the RAIR ship in orbit around Ceres -- which you used for this piece. Forgive me for fangirling, but it was pretty exciting to come across a piece of my own art on this page, since usually I'm just here to pinch your ideas. If you ever need someone to take a crack at making art for a post, feel free to let me know.
Alright, alright, enough of that. On to my question.
I noticed that the design you propose here relies on impact-ignited fusion, which means highway-riding ships (skaters? riders? maybe we need a term for these vessels) have to carry lots of inert mass in order to ride the highways -- the sort of thing that makes my rocket equation senses tingle. IIRC similar results could be achieved using an onboard magnetic field to compress and ignite the fuel pellets. Is the reason you went for impact-ignited fusion to increase the power density of the drive, or is there another reason for this design choice?
Thanks for your time, and keep up the great work.
Best regards,
Lilly Harper
Oh, that's awesome! Accurate artwork of realistic spaceship designs is sadly very rare, so thanks for doing it. Do you have a link to more of your work?
DeleteThe whole point of the Fusion Highway is that the riders carry *very little* onboard propellant. In the modest example, the spaceship carries 11 tons of target masses, which is enough to ignite over 5000 tons of fuel pellets.
You could use conventional ignition methods to ignite the fuel pellets, but you're losing out. An onboard ignition system like magnetic compression uses the same amount of energy to compress the same amount of fuel all the time, and it only gets harder as the relative velocity between spaceship and the Fusion Highway (hard to compress something sweeping through your reaction chamber at several hundred km/s!). However, impact ignition uses the fuel pellets' own kinetic energy for ignition, so you need basically no onboard equipment and it only gets easier as the relative velocity increases...
Hey, Matterbeam, thanks for getting back to me.
DeleteYeah, I post my art and fiction to my site beaconsinthedark.wordpress.com on a (mostly...) regular basis. I've been meaning to get around to posting my animation of your Epstein Drive fusion torch design, actually -- and a render I've made of your hydrogen stealth steamer. Shoot me an email through my site's contact form and I'll be happy to send them both over to you.
As for impact-ignition, that makes a lot of sense -- it's something I feel a little silly for not having thought of beforehand. I guess I've still got the Atomic Rockets bug, constantly looking to cut down on a ship's mass, haha.
With regards to the fusion highway, how much potential is there for weaponisation? I'd imagine that a stream of high-speed fusion fuel might be the sort of thing authorities might want to control -- it strikes me that those pesky Belters could quite easily defend themselves from a more professional, formalised naval power. Would a dust shield, like you described in your Macron posts, be enough to protect a vessel from the wrongful use of a fusion highway?
Thanks for your time.
I've been reading through your website. There are some really great hard sci-fi stories in there!
DeleteI'll contact you about the art on your contact form.
Impact ignition is not very popular today as is barely ever mentioned when discussing fusion energy, so you're excused.
A Fusion Highway isn't dangerous by itself. It is slow, huge and cannot reorient itself. The fuel pellets might be travelling at 100km/s+, but that is much slower than the spaceships zipping around and would take many months to years to reach far away targets. They are no more a weapon than their launch platform is! You could easily disable a highway by zapping at its fuel pellets one by one.
It's what rides the highway that is important. For example, a sort of drone rider that handle many g's of acceleration can shoot off a payload of missiles at several thousand km/s. It won't be faster than a regular spaceship riding the highway to maximum velocity, but it can be accomplished with much smaller runways. That's enough to make it an interplanetary weapon. The launch itself and the direction the missiles take would be very visible to everyone, and they'd give a few days of warning to the target, but the missiles could cool down and become stealthy during the transit.
However, if you run the numbers, you'll find that even these short high-g launches take place over several hours and millions of km. 'Wrongful use' is very much a planned, coordinated event.
Not sure if you are aware of this, but I found a paper on impact fusion in "Atomic Rockets":
ReplyDeletehttp://www.projectrho.com/public_html/rocket/supplement/Impact%20Fusion%20Write-Up.pdf
Thanks for that! I had heard that there was the potential for 'clean' nuke that only used chemical explosives and fusion fuel, but I hadn't come across the paper for it.
DeleteThanks, Thucydides. I wonder: could this technology could be used to create a more efficient/powerful Kasaba Howitzer, aka, "Thermonuclear Plasma Cannon" (TPC)"?
ReplyDeleteAlso, ISTM that the Fusion Highway would require substantial IP traffic to be economical- how much IP traffic would be required, what types of activity (commercial, military) would require that much/what are the optimal types of traffic to use the FH, etc.?
Not to sure if this would be any improvement over a Casaba howitzer. You would need some sort of device to slam the pellets together at the time and place of your choosing - Matterbeam has a post about impact fusion as an engine - but it would be incredibly large and bulky as the "physics package" - the expanding plasma and X ray radiation needs to be funneled and focused as well, a filler channel seems to be needed to moderate the radiation and then the actual "warhead" part being weaponized is attached to the front. Since you essentially have two honking railguns pointed at each other you would probably have more bang for the buck just shooting the target directly (and the railguns can be used more than once).
ReplyDeleteAlternately, you could have your ship mounted railgun fire a pellet at the "physics package" on the Casaba Howitzer to initiate the fusion reaction, but I suspect that the extra uncertainties of getting a precise strike and clean fusion burn might argue against this. A slight miss could lead to the destruction of the Casaba Howitzer rather than its initiation.
As for the amount of traffic needed, that would have to depend largely on the initial cost of the system. The more traffic you have, the lower the price you can charge your customer since you can amortize the cost over a large number of ships. The same logic applies to any sort of similar system - shooting cargo pods from a mass driver, a Kare "sailbeam" or even using lasers to propel lightsails. You probably could charge a premium given the much higher velocities of a fusion driven ship, but the ships themselves would be more expensive as well - a very detailed calculus would be needed to see which system has the better economics.
My own personal take on this is that laser sails and mass drivers are the more likely candidates, since they are extrapolations of demonstrated and existing technology, can have multiple uses (the laser can be used to sell energy by beaming it across the Solar system, for example) and seem generally more flexible. YMMV.
The problem with igniting a Casaba Howitzer warhead externally is that you want to deploy it as far as possible from yourself. Crossing that distance with a high velocity projectile is going to add a huge delay to your attack, as well as additional constraints, such as the warhead only being able to fire are targets that are generally aligned with the projectile weapon.
DeleteAs I stated before, a Fusion Highway and related technologies are not easily weaponizable.
I agree with all your other points!
I think I have a solution for the "Minimum Safe Distance" issue with casaba howitzers: You could hypothetically take a large "recoilless rifle" type device, give its interior surfaces a thick spray-on ablative coating, and use a low yield narrow angle casaba as the propellant charge. Combine this concept with a light gas gun and you could potentially achieve some truly stupendous muzzle velocities even with very heavy projectiles, while also being able to fire "blanks" to utilize the enormous muzzle blast/backblast for point defence. Swap out the light gas gun for an appropriately designed aperture and you now have a reusable bomb pumped laser.
DeleteSeveral aspects of this fascinating scheme remind me of the Orion Drive.
ReplyDeleteGiven that Projekt Orion created the Casabla Howitzer, because focusing the nuclear explosion was beneficial, could the fusion highway benefit from shaping its nuclear explosions? Or would the difficulties of getting the ignition mass through the structure of a shaped explosive instead of just onto a plain fuel pellet be too great?
You mention that one can combine this drive with others to get more flexibility. Am I correct in assuming that one could simply feed this drive with orion pulse units? That would also solve the issue of acceleration highways. Alternatively the acceleration highways could be plain old nukes, circumventing the need for high initial velocities. Especially the pure fusion bombs mentioned earlier in the comments could be very interesting in such a setup.
One of several major problems with an interstellar probe is how to slow down at the end of the trip. This fusion highway concept offers a way around that.
ReplyDeleteInstead of launching just one probe, launch a series of pellet tenders first. The pellets themselves need to be decelerated to below the probe's expected velocity and the design impact speed. A macron accelerator on the tender should be able to provide about 10,000 km/s of delta-V to the pellets through fusion-boosted ablation, which for a 0.2 c cruise velocity means six stages of tender are required for the final set of deceleration pellets (and one less for each earlier set).
That in turn means launching 21 tenders to bring 1 probe to rest. That may sound like a huge investment, and it is, but the probe then has an effective mass ratio of 1. As an alternative, if the probe has its own macron-based fusion engine and a mass ratio of about 4 then it should only take three stages of tender (6 in total).
I'm thinking on the order of hundreds of tonnes mass for the probe, enough for multiply-redundant systems, decent comms bandwidth back to Sol and delta-v to maneuver around the system for a bit. There's also quite a bit of shielding required to survive the trip.
It would be quite expensive, not to mention roughly 30 years from flight readiness to first data returns. I think in a setting where vehicles are routinely traveling on fusion highways, a mission like this could be done for a reasonable fraction of overall travel costs and much of the propulsion engineering would already be done. Might even be before the end of the century.
I haven't expanded on the interstellar aspect as I'm gathering material for a Part 2 to this concept.
DeleteBut you are on the right track: I am thinking of 'staged' Fusion Highways where the pellet track is laid down at relativistic speeds so that an even faster craft can travel on it. It can also be paired with other relativistic propulsion schemes to create a system which has no weaknesses, only strengths.
Hi, Matterbeam.
ReplyDeleteCan you please explain how the fusion highway rider drive works in supercritical "kinetic band" regime ? Especially if the fuel pellets no longer contain any fuel.
Where does the power come from in "kinetic band" regime using inert track pellets ?
Does "kinetic band" require target pellets to contain thermonuclear fuel instead of track pellets ?
How does "kinetic band" regime of the highway compare to Daedalus style fusion drive ?
The power comes from the relative velocity between the spaceship and the track.
ReplyDeleteIn an indirect way, you are extracting that energy with an impact and redirecting it using magnetic fields. This is a bit similar to how the 'Blackbird' wind vehicle functions. Veritasium did a video on it!
The ship converts the kinetic energy of the large target masses into ships kinetic energy.
DeleteSo, in kinetic regime it looks like ordinary rocket where target masses are both fuel and propellant. The track masses provides the ignition of the target masses.
That's right.
DeleteSince orion type drives have smaller effective exhaust veilocities, would this "crumb line of nukes" work there?
ReplyDeleteYes, it would work, but only lower velocities could be achieved.
DeleteA similar concept is discussed here
ReplyDelete1. http://moofrnk.com/assets/files/journals/science-prospects/43/science-prospects-4(43)-2013.pdf pp. 56-66
2. http://lnfm1.sai.msu.ru/SETI/koi/articles/86.pdf
3. http://alpha.sinp.msu.ru/~panov/KinEngine-Panov-2-W.pdf
4. http://www.sciteclibrary.ru/texsts/rus/stat/st5860.pdf
5. http://lnfm1.sai.msu.ru/SETI/koi/articles/Zotiev-Podvysotsky-2014-04-08.pdf
6. http://lnfm1.sai.msu.ru/SETI/koi/articles/Zotiev-2014-03-25.pdf
7. http://lnfm1.sai.msu.ru/SETI/koi/media/Podvysockiy.pdf
8. http://n-t.ru/tp/ts/kd3.htm
9. http://n-t.ru/tp/rz/spukd.htm
Thanks for these!
DeleteCriticism of the details of this scheme:
ReplyDeletehttps://vk.com/wall-147618894_1169
You can read it using the google translate service
This is such a great concept! But can you elaborate more on how to keep Deuterium fuel pellets solid in space in the inner solar system? Especially if they contain Tritium that produces heat via radioactive decay.
ReplyDeleteI've been pondering ths concept for a while now. I believe I've come up with an improvement that solves the track entry issue as well as the issue of the beamrider carrying target masses. Just use two converging beams that almost collide. The beamrider can steer the projectiles into a collision using on-board equippment. A nice side effect of this is that it decreases the demands on the track laying systems or allows you to double the impact velocity at hand.
ReplyDeleteAdditionally, a single track laying mass driver could even lay both tracks if the time and mission demands allow you to make use of orbital mechanics to lay the incoming part of the track.
I wonder if this makes the interstellar versions more viable, even if one is only using accelerators in the Kuiper or Oort Regions. If this idea works in the first place. How the post about the interstellar version of this coming along by the way?
Keep up the great work, you have really changed the way I see future techology.
This comment has been removed by the author.
ReplyDeleteTritium decays and puts out about 324 W/kg of beta-radiation. So it won't stay frozen or liquid for very long.
DeleteI guess it would have to be actively chilled until release, or be accompanied by a hydrogen heatsink.
DeleteHow would this work in interstellar combat? You've got you "fusion road' laid out ahead of time, but what if down the road (so to speak) someone/something found it and tried to disrupt or hijack it somehow? (Cue the space pirates...)
ReplyDeleteThis IMO is why any interstellar civilization worth its weight in dark matter (such as it is) will probably still use ion fusion drives (or maybe one of those fancy Kip Thorn wormhole thingys) for travel.
Starship on the fusion highway don't fight each other, the same way trains on railways don't go to battle. You need independent propulsion that takes you anywhere on your own schedule to enter combat.
DeleteOf course, you might have your Fusion Highway rider carry smaller combat craft to defend itself.
I was wondering, could such a propulsion system be applied to a tensile spaceship (picture the ISV from Avatar)?
ReplyDeleteYou can imagine the magnet that catches the fusion explosion plasma as a ring structure that you 'hang' your payload from. Think more 'chandelier' than 'pendulum'.
Delete