Reset your expectations of solar sails. They are a fast and free way to travel to any point in the Solar System, as many times as you want, any time of the year.
Solar sails can carry passengers and they have a nearly unlimited number of uses. You just have to... think big!
Solar Sails
Art by Stepan Polivanov.
Sunlight is abundant. The energy needs of any activity can be met by simply collecting enough of it. All of human civilization, for example, could be powered by the perfectly using the sunlight passing through an 86 km square near Earth. There’s more than enough sunlight to power space travel. How convenient that we can just harvest what we need to get anywhere in the solar system!
The usual approach is to use photovoltaic devices. They convert sunlight into electricity, which can then power electrical devices directly. They’ve had a long history: the first solar panels in space were launched with Vanguard 1 in 1958. Those panels produced 1 Watt in total. Today, the largest solar-powered installation in orbit is the International Space Station. Its eight arrays could generate up to 240 kW when new.
Accumulated damage from micrometeorites and radiation will necessitate their gradual replacement though. The latest development is the large-scale use of electric thrusters. The DART mission used the NEXT-C thruster at a 3.5 kW power level, and thousands of Hall-effect thrusters are deployed with the SpaceX Starlink constellation.
However, solar panels are not the only way to make use of solar power. Solar sails directly convert sunlight into thrust. Their efficiency usually exceeds 90% and they’re very resistant to degradation.
A spacecraft equipped with these sails can accelerate endlessly without requiring a drop of propellant. How is this possible? How much acceleration can be achieved? How far can we push this technology? Let’s dive into these questions in the following sections.
Light and Speed
 |
| Space sailing! By Jett Furr. |
The way a solar sail works is pretty simple. Light has no mass but it has momentum. When it strikes a surface, it generates radiation pressure proportionate to its intensity. If the surface is reflective, that pressure can nearly be doubled.
An equation describes radiation pressure:
- Radiation Pressure = Light Intensity x (1 + Reflectivity) / C
You can convert radiation pressure into thrust if you know the area of the reflective surface.
- Radiation Thrust = Radiation Pressure x Area
A square solar sail that’s 10m on each side would have an area of 100 m^2. Following the previous example, it is feeling a pressure of 8.6 microPascals. The total thrust it generates is 8.6 x 10^-6 x 100 = 8.6 x 10^-4 or 0.86 milliNewtons. That’s not a lot of thrust; it’s equivalent to the weight of 3 grains of rice.
From thrust, we can work out acceleration if we know the mass of the sail. The mass of a sail is related to its area: usually a sail with 10x the area is also 10x heavier. We’ll therefore use the area density.
- Solar Sail Acceleration = Radiation Thrust / (Area Density x Area)
A typical area density for today’s solar sails is 10 grams per square meter, or 0.01 kg/m^2, as found on the IKAROS sail. A 100 m^2 sail would therefore mass 1 kg. The acceleration we can expect from 0.86 milliNewtons of thrust is 0.00086 m/s^2, or 0.086 milligee. It would take this sail nearly two minutes to gain 1 m/s. In more familiar terms: its “0-100 km/h” time is 9 hours!
If we combine all the previous equations, we can write:
- Sail Acceleration = Light Intensity x (1 + Reflectivity) / (C x Area Density)
Notice how ‘Area’ disappears from the equation. A bigger sail will not accelerate faster. Improving reflectivity does not affect acceleration much as the difference between a good 90% reflectivity and an incredible 99.999% reflectivity is small. That leaves two factors that really affect acceleration: Light Intensity and Area Density. Light Intensity varies between 64 MW/m^2 at the surface of the Sun to 0.873 W/m^2 near Pluto. Increasing that figure means getting closer to the Sun, but that might not always be where you’re headed. Area Density is the only contributor to sail acceleration that we can really affect.
In the example we used, we ended up with a solar sail that accelerates about four times slower than a snail because it only had access to Earth-levels of sunlight and had a 0.01 kg/m^2 mass per area. If we attach a payload to that sail, it will accelerate even more slowly.
 |
| Angles relevant to a solar sail. |
What’s more, conventional solar sails can only reflect sunlight back in the direction it came from or off to the side. For a spacecraft trying to spiral out of its current orbit then into a new one, this is a problem. It will have to angle its solar sail to produce sideways thrust to increase its orbital velocity. The efficient angle is 35° to the Sun. At this angle, the sail’s ‘effective thrust’ is actually 82% of maximum as it is not fully facing the Sun.
The result is a space vehicle that takes months to years to accomplish the most minor of maneuvers, let alone interplanetary transfers that require deltaV changes in the thousands of m/s. This is currently acceptable for small probes that can fit inside rocket upper stages as secondary payloads.
But can we do better?
Less is More
 |
| Lightsail 2's deployment. |
The material that today’s solar sails are made of is aluminized Mylar supported by extensible trusses. It is only a few micrometers thick (7.5 micrometers in the case of IKAROS) and manages to reflect 90% of sunlight.
 |
| 2 micrometer thick aluminized PEN being spooled and handled manually |
The main struggle is getting a reflective surface that can be packaged like origami into a very small volume, survive the vibrations of a rocket launch, then reliably deploy out in space into a rigid structure.
 |
| Solar sail deployment |
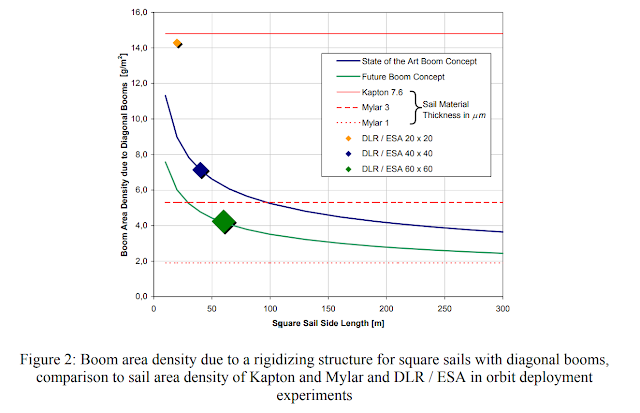
Also, since solar sails so far have been of modest size, the mass of secondary equipment like control actuators or deployment mechanisms take up a proportionally larger fraction of total mass. Simply making larger sails will improve their area density. They also need features to prevent tears from ripping through the entire sail, or to keep edges of the sail material from curling inwards.
The first step to improving area density is to take current materials and improve them. The DLR/ESA 60m sail is an example of a realistic near-term goal. Reducing Mylar sheet thickness to just 3 micrometers could reduce area density to 4.2 g/m^2. Add in the mass of the aluminium coating and the graphite booms and you achieve 5.3 g/m^2. The Encounter sail is even larger, and projected Mylar sheets of just 1 micrometer thickness, for an overall area density of 1.9 g/m^2.
Another avenue to reduce area density is to cut away solid support structures in favour of other ways to keep the sail to its intended shape. Inflatable booms can be lighter than graphite rods. Rotating sails can be lighter still - they can use centripetal forces to both extend the sail and to keep it under tension. These result in circular sails, or even ‘heliogyros’ where the sail is divided into ‘blades’ kept under tension like a helicopter’s rotor. Controlling their motion is more complicated though.
 |
| A heliogyro sail catching up to Halley's Comet. |
If we put together the thinner materials and innovative configurations, we are likely to achieve sails with 1 g/m^2 area density. This would grant them accelerations on the order of 0.86 milligee, likely to be 0.5 milligee with payload included. That’s enough to get a spacecraft from geostationary orbit to Earth escape in about a week.
But we can do even better.
A better material than Mylar can be considered. Carbon fibers supporting an aluminium layer can achieve 0.5 g/m^2 or better.
At some point, we can imagine removing the supporting layer entirely and relying instead on the metal reflector alone. This layer can be very thin: as low as 0.14 micrometres in this proposed example. It is a way to achieve sails with an area density of 0.33 g/m^2, rising to 0.45 g/m^2 when including support booms.
Nanotechnology can come to our aid.
Sub-wavelength metasurfaces allow solar sails to remain reflective while having gaps smaller than the wavelengths of sunlight. It is similar to how the metal screen in your microwave oven’s door reflects the 2.45 GHz (12.2 cm) wavelengths inside but lets visual wavelengths (0.4 to 0.7 micrometers) through. A solar sail can use the same concept to become mostly empty space while remaining reflective. The shortest wavelength we want to capture would be 0.4 micrometers, so we could use a quarter-wavelength grid spacing of 0.1 micrometers (so it would be 75% empty). That would reduce the sail mass four-fold, down to 0.1 g/m^2.
 |
| More advanced sail configurations. |
Theoretically, we can shave down the reflective surface down to the absolute minimum thickness that can interact with sunlight. This seems to be 10 nanometers for Aluminium. A sail of that thickness would have an area density of 0.027 g/m^2. If we further apply the sub-wavelength gaps, we could bring it down to the level of 0.01 g/m^2. That would enable accelerations on the order of 87 milligee.
But it comes with many downsides. This sort of ultra-thin surface is very weak (tensile strength of 0.225 Pa) so while it would survive the radiation pressure of the Sun, it might not handle any other sort of disturbance. It would also become vulnerable to the ambient space environment: solar wind, interplanetary dust, radiation damage and so on.
.jpg) |
| Radiation damage to solar sail surfaces. |
Better performance can be achieved if we abandon reflective sails and use diffraction instead.
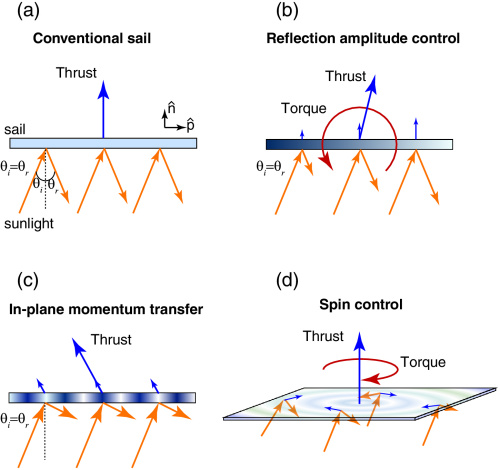 |
| The many ways a diffractive sail can manipulate light. |
Diffractive sails let sunlight pass through them while bending the angle at which it emerges, which produces a force at the opposite angle. If they bend sunlight to the right, they feel recoil from the left. Diffraction gratings made with very thin transparent materials like silica, or reflective strips made of aluminium spaced by about a micrometer, can do the job. There are few details on how such a grating could be constructed, but they are often directly compared to conventional sails in terms of area density.
 |
| Diffractive sail thrust. |
The most interesting feature is that control of their optical properties (switching the angle of the grating, for example) allows them to redirect that sunlight in any direction, and therefore control the direction of their thrust. Conventional sails can only accelerate away from the Sun or at an angle away from it. Refractive sails would work more like an engine in that they can choose with direction to accelerate. They can do this with over 90% of the energy they gather, as described here. This allows the sail to always point at the Sun for maximum efficiency while thrusting sideways or even towards it. Advanced control would even allow them to discard control thrusters or control gyroscopes for further mass savings.
 |
| A 'photon thruster' sail. |
Another interesting configuration for solar sails is the ‘photon thruster’. It’s essentially a set of two mirrors working together: one large collector and a smaller mobile mirror to redirect the light in any direction. The advantages are a much wider range of maneuvers that become possible, and since the collector mirror can always face the Sun directly, there is no loss of efficiency from angling the thrust. The downside is increased complexity and the additional weight of the mobile mirror.
There are even more speculative types of solar sail, but their applications are limited.
‘Black sails’, for example, absorb sunlight. They do not reflect or redirect the sunlight, so they only accelerate away from the Sun (try using the equations above with R=0). It’s useful for well timed exploration of the outer solar system or interstellar missions, but not much else. The upside is that they can use the thinnest and strongest materials available: carbon nanomaterials. Their very low density works in their favour. Aerographite, for example, has a density of just 0.18 kg/m^3. A 1 mm layer of it is opaque and could create a solar sail with an area density of 0.18 g/m^2. It is unclear whether it remains opaque at 0.1 mm thickness, which translates to 0.018 g/m^2. The potential acceleration would be as high as 0.25 m/s^2.
 |
| A 3mm wide graphene light sail under testing |
At the material limit, we have a single layer of graphene. It’s just one atom thick (0.345 nanometers) and its area density would be 0.00077 g/m^2. However, pure graphene only absorbs 2% of sunlight while letting the rest through. That limits its acceleration to 0.12 m/s^2 near Earth. It has been suggested that adding a layer of Molybdenum disulfide (MoS2) can increase the absorption to 37% of sunlight. The area density of a graphene/MoS2 bilayer would increase to 0.004 g/m^2 allowing its potential acceleration to become 0.4 m/s^2.
It’s also possible to create black sails with area density below the material limit, by using dusty plasmas. These sails would magnetically confine a plasma that can hold charged particles within itself. Those particles would absorb sunlight. Since plasma sails can grow to immense sizes of several tens of kilometers in diameter, with very little mass within them, they effectively constitute solar sails with area density as little as 0.001 g/m^2 or less. Few studies have focused on dusty plasmas or their characteristics, so there is no data on their sunlight-absorbing properties. We therefore can’t guess at their potential acceleration.
The Sails
Let’s design four solar sails to use as a reference for the rest of this post. They’re meant for increasing payloads and more demanding missions with each technology level. Note that we’re adding 20% to the area density to account for all the other equipment a sailcraft needs to navigate.
Characteristic Acceleration is the acceleration the sail manages when receiving full illumination at Earth sunlight levels (1361 W/m^2).
Modern Sail
Advanced Heliogyro Sail
This sail is made of six blades rotating around a central truss. Thanks to its Mylar layer being thinned to 1 micrometer, its area density is much improved over the Modern Sail. It’s small enough to fit into the secondary payloads of a regular rocket like a Falcon 9 on a geostationary transfer orbit mission.
Nanofilm Sail
This sail uses a reflective surface that’s just a tenth of a micrometer thick, further lightened with sub-wavelength holes. Carbon nanotube struts hold it up into a 2000 m wide square. Since some shorter wavelengths pass through its holes, it has a reduced sunlight interaction efficiency. At this scale, it is matching the useful payloads of deep space probes while requiring only a fraction of the initial mass. Launching it up from the ground is a dubious proposition though.
Diffractive Meta-Sail
This sail is 50 km wide. Despite its immense size, it’s still only the equivalent of the payload of a single heavy lift rocket today. The sail surface is a nanostructured diffraction grating about 10 nanometers thick, actively controlled by piezoelectric actuators to be able to give complex shapes to the sunlight that passes through it. Its sunlight interaction efficiency is 90% as it does not reflect the light but merely redirects it. This is a sail large enough to transport humans on interplanetary missions. However, it is certainly too fragile to be launched atop a rocket or even folded before deployment. The whole structure would have to be assembled in orbit.
Solar trajectories
The most important aspect of solar sail travel is the sail’s acceleration relative to the local gravity.
 |
| A sail with very low acceleration spiralling out of LEO to escape velocity |
In Low Earth Orbit, local gravity is quite similar to the 1g found on the surface. Solar sail acceleration would be much much smaller than the local gravity. The Modern Sail would have an acceleration of 0.039 milligees, for example.
In this environment, solar sails can only make very gradual spiralling trajectories as they attempt to raise or lower their orbit. A useful approximation for how long this takes is to divide the difference between the initial and destination orbits’ velocities by the sail’s acceleration.
Let’s try it. The orbital velocity at 1000 km altitude is 7350 m/s. The orbit velocity at 35,800 km (geostationary) altitude is 3075 m/s. The difference is 4275 m/s. The Modern Sail would take 4275/0.00039 = 10,961,538 seconds or about 4.16 months to complete the maneuver. Realistically, it will take a while longer as we have not accounted for the time spent in Earth’s shadow, the inefficiencies from accelerating sideways to the sunlight and the effects of atmospheric drag, which can be significant even far above the atmosphere.
The Advanced Heliogyro Sail with its 0.0019 m/s^2 acceleration would do it in 26 days.
This approximation holds true so long as sail acceleration is far below local gravity.
In the following table, epsilon E is the ratio between the spacecraft’s acceleration and local gravity. The third column is the ratio between the deltaV needed to reach escape velocity, and the initial orbital velocity. And in the fourth column, we have the number of orbits needed to complete the maneuver.
When E is very low (10^-5), we have to expend practically as much deltaV as our current orbital velocity to escape into deep space. In this specific example, your deltaV requirement is 95.75% of your current orbital velocity. It also takes an incredible number of orbits to complete this sort of maneuver (over 50,000!).
As E increases, you need less deltaV and less orbits to reach escape velocity. When E is a hundredth (10^-2) of local gravity, you only need to spend 76% of current orbital velocity to escape and it takes just 51 orbits to do this. While deltaV savings don’t mean much to a solar sail, they do translate into additional time savings.
However, you will notice that solar sails with the performance levels we find interesting will achieve accelerations comparable to or exceeding local gravity. Consider what happens as we move away from Earth. At an altitude of 100,000 km, the local gravity is 0.035 m/s^2. At 400,000 km, or 1 lunar distance, it is only 0.0024 m/s^2. Compare these values to the accelerations that advanced solar sail designs can achieve. The Advanced Heliogyro Sail manages 0.79 times the local gravity at 1 lunar distance. That’s a ‘thrust to weight’ ratio we typically find on fighter jets! In other words, high performance sails can pull off acrobatic maneuvers, albeit in slow motion from our perspective.
Throughout the rest of the solar system, we have this useful chart:
At 1 AU from the Sun, solar gravity is 0.0059 m/s^2. At 5.2 AU (Jupiter’s orbit), it falls to 0.00022 m/s^2.
Note that the Sun’s gravity and the intensity of sunlight follow the same inverse square scaling with distance (D^-2). Intensity of sunlight determines a sail’s acceleration. Therefore, a solar sail will always maintain the same ratio of acceleration to gravity, regardless of how far it is from the Sun. We call this the sail’s beta B or ‘lightness ratio’.
For example, if a sail manages an acceleration of 0.001 m/s^2 at 1 AU, which is six times lower than solar gravity, then it will achieve 0.000037 m/s^2 near Jupiter, which is also six times lower than solar gravity over there.
Small lightness ratios leads to very long travel times. A ratio of 0.015, which is an acceleration of around 0.00008 m/s^2 near Earth, would mean an annoying long transfer time of 1647 days to Mars. That’s 4.5 years.
Increasing the lightness ratio dramatically shortens travel times. It makes solar sails act more like powerful rockets. A lightness ratio of 0.1 is enough to take on fast trajectories to Mars.
176 days is about 6 months, which is shorter than the usual 9 month Hohmann transfer chemical rockets can manage. And unlike regular rockets, a solar sail can make its way from Earth to Mars or back without having to wait for any transfer windows. Another study shows that a Mars mission can take less than 120 days using sails with a lightness ratio as low as 0.2. However, that involved meeting Mars with a velocity of 5-12 km/s. An Advanced Heliogyro sail would make up that velocity gap in 70-170 days. The other option, as the study suggests, is aerocapture into Mars orbit.
We can reasonably assume that sails in that performance category can complete trips to the Outer Planets at least as fast as minimum energy Hohmann transfers: 2.7 years to Jupiter, 6 years to Saturn.
 |
| Solar sails are relatively quick even with low performance levels. |
But if we increase performance to a lightness ratio of 0.5, we would enable a solar sail to directly move away from the Sun and accelerate onto a solar escape trajectory that eventually resembles a straight line into interstellar space.
We have this trajectory for a sail with a lightness ratio of 0.6, where it takes 2.8 years to reach Jupiter:
The same paper finds an 11.5 year trajectory to Saturn with a lightness ratio of 0.5:
 |
| The trajectories possible with different lightness ratios. |
With a lightness ratio exceeding one, a solar sail can take that initial orbital velocity and add to it. It can shorten the trip by many months. The Nanofilm Sail has a lightness ratio of 3.73. It can keep accelerating towards a target like Jupiter, crossing the 4.2 AU minimum distance to that planet in 103 days. At the end of the trip, it is travelling at 85.8 km/s. The Diffractive Meta-Sail has a lightness ratio of 44. It completes that same trip to Jupiter in 37 days, reaching a velocity of 253.1 km/s by the end of it. Those same sails can reach Saturn in 203 days and 66 days respectively.
 |
| A solar sail cannot accelerate into the Sun. |
Of course, just zipping past your destination isn’t always desirable. A sail can just turn itself edge-on to the Sun to stop accelerating away from it and let gravity take over. Solar gravity is however very weak. The sail performance doesn’t really matter in that case: the trip always takes about 630 days (1.72 years). For Saturn it is 1660 days (4.5 years). Caution! These are only rough calculations that have to be taken with a grain of salt, as they are basically assuming the sail makes a straight line for its target and stops at the end with near-zero velocity. A realistic trajectory, such as one that tries to reduce the relative velocity during the encounter with Jupiter (13 km/s) or Saturn (9.7 km/s) will be different and might take a bit longer. Still, they are much faster than minimum energy Hohmann transfers, and they can be launched any time during half the year where Earth and the target planet are on the same side of the solar system.
Now, there are tricks to make those trips shorter.
 |
| From "Multiple-satellite-aided capture trajectories at Jupiter using the Laplace resonance" |
Jupiter and Saturn have large moons that can help capture a solar sail into an orbit around the gas giants. Gravity assists can change the velocity of a passing spacecraft by a maximum of twice the planet or moon’s orbital velocity. The Moon, for example, orbits Earth at about 1 km/s, so theoretically it could grant a velocity change of up to 2 km/s. Lunar Gravity Assists have been calculated to provide 1.5 km/s of deltaV savings for capturing asteroids into Earth orbit from a single pass.
 |
| Earth's Moon used for gravity assists and slingshots. |
We can therefore expect proportional deltaV savings from other large moons. Jupiter has Io, which orbits at 17.3 km/s. A Nanofilm Sail that only has to slow down to 17.3 km/s before reaching Jupiter could shorten its trip time to 312 days (-50%). If Enceladus and its 12.6 km/s orbital velocity can be used to capture into Saturn, then the Nanofilm Sail’s trip is reduced by 51% to 814 days. Again, gravity assists are much more complicated than this but we do get a rough estimate for what sort of benefits we get from them.
 |
| A solar sail at Saturn |
Returning from the gas giants is not easy. It takes a very long time to maneuver far from the Sun, and even in the best case afterwards, only solar gravity can pull the sails inwards. For example, the Nanofilm sail has an acceleration of 0.000813 m/s^2 near Jupiter. It would take it around 185 days to cancel out Jupiter’s orbit velocity and start falling straight into the Sun. From a distance of 5.2 AU, it would ‘fall’ for 740 days until it is at a 1 AU distance from the Sun. Intercepting Earth is done near the Sun, using maneuvers that take up to 25 additional days. The total mission time is therefore 950 days or 2.6 years. That’s only slightly faster than a Hohmann transfer. Using a better sail can shorten the 185 day and 25 day portions of the trip, but does nothing to the 740 day freefall period.
Inner solar system missions don’t have to cover as much distance as missions to the gas giants, but they do have to contend with targets that have much higher orbital velocities: Venus at 35 km/s and Mercury at 47 km/s. Neither of them has a useful moon for gravity assists either. Capture into those planetary systems is therefore quite challenging.
 |
| A Mercury sample return mission. |
For low performance solar sails, we expect to see slow spiralling trajectories. Thankfully, their acceleration increases as they get closer to the Sun. On the way to Venus, a solar sail’s acceleration nearly doubles. The average acceleration is 145% of its characteristic acceleration. Near Mercury, a solar sail is zipping around at 6.7 times its characteristic acceleration. A sail’s average acceleration is 383% its Earth-normal acceleration on the way to Mercury.
We have here data on Venus transfers with a sail of characteristic acceleration of 0.1, 1 or 2 mm/s^2. That’s lightness ratios of 0.017, 0.17 and 0.34. We see that increasing performance brings the transfer time closer to the Hohmann minimum-energy trajectory that takes 146 days to Venus.
Mercury remains a challenging target for low performance sails. One way around that is a flyby of Venus to shorten the travel time to the innermost planet. We can see significant benefits for sails with lightness ratio below 0.1.
 |
| Venus flyby on the way to Mercury. |
Another paper studies interplanetary trajectories for a diffractive sail. The range of characteristic accelerations is 0.1 to 1 mm/s^2. Surprisingly, it takes about the same amount of time to reach Venus as it does Mercury; about 200 days.
To Venus:
To Mercury:
High performance sails with excellent lightness ratios have similar troubles with the inner planets as they do returning from the outer planets. It’s the ‘cannot fall inwards faster than gravity’ problem. Even if they cancel out all of their orbital velocity, they can only be pulled inwards by the relatively weak solar gravity.
At Earth’s orbit of 1 AU, solar gravity is 0.0059 m/s^2. Near Venus’ 0.72 AU, it is 0.0113 m/s^2. Mercury is the closest to the Sun at 0.39 AU and experiences 0.0387 m/s^2 of solar gravity.
We can use a table to calculate the position of an object falling into the Sun every 1 hour. It should take about 42 days to fall from Earth to Venus, accumulating about 26 km/s of velocity by the end of it. Falling from Earth to mercury takes 57 days, reaching 52.5 km/s. Falling all the way into the Sun takes 65 days, which matches theoretical results.
The direct trajectory that gives the minimum possible travel time from Earth to Venus or Mercury for a high performance solar sail is the following: cancel out Earth’s orbital velocity (29.78 km/s), fall to the desired altitude, cancel out the accumulated fall velocity, accelerate to the target’s orbital velocity.
For a Nanofilm sail travelling to Venus, the Earth maneuver takes 15.7 days. Falling towards Venus takes 42 days. Cancelling out the 26 km/s inwards velocity and gaining the planet’s 35 km/s orbital velocity take together (26,000+35,000)/(0.022 x 1.91): 16.8 days. The total trip is 58.5 days before optimizations.
A high-tech Diffractive Meta-sail travelling to Mercury would cancel out Earth’s orbital velocity in 1.3 days. It then falls for 57 days. Removing the 52.5 km/s inwards velocity and catching up to Mercury orbiting at 45 km/s can be done in one intense 97.5 km/s maneuver. It is made more manageable by the 3.83x boost to sail acceleration nearer the Sun, so it only takes (97,500)/(0.26 x 3.83): 1.1 days. The total trip duration is 59.4 days, with 96% of the time spent just falling towards the Sun. Returning from Venus or Mercury to Earth is like to be even faster.
 |
| 'Sundiver' maneuvers with a sail |
You may have noticed how much faster sails get when they approach the Sun. The fact is exploited fully with the SunDiver maneuver (also called a solar photonic assist), where sails get to within 0.1 AU of the Sun for a massive 100x increase to their characteristic acceleration.
 |
| Even a sail with a modest lightness ratio of 0.3 can reach Neptune in 933 days thanks to a single SunDiver maneuver. |
 |
| Characteristics of an aerographite spherical sail |
At the upper limit, using carbon nanomaterials like Aerographite, we can push solar sails to 2% of the speed of light. Of course, there is no way to stop these sails afterwards. They can fly past planetary targets or simply head out into interstellar space.
.png) |
| 'Pole sitter' statite |
Finally, high performance solar sails, especially designs with a lightness ratio equal or exceeding one, have the notable ability to just… stop. They can hover in any place. This turns them into ‘statites’; stationary satellites. These are useful if you want to place an observatory or telescope in an exact position or lay down a fusion highway.
 |
| A solar sail following a 'displaced orbit' |
A high performance sail could also enter ‘short orbits’ that only partially cancel out gravity near a planet, or follow complex trajectories (neither lines nor orbits) that take them between arbitrary points in space, like sitting exactly halfway between the Moon and Earth or above a specific crater on a spinning asteroid. Since they need no propellant, they can keep this up indefinitely.
Hybrid Braking
So far we have talked about solar sails exclusively using sunlight for propulsion. This doesn’t have to be the case. ‘Hybrid sails’ use a mix of propulsion systems.
 |
| OKEANOS combines a solar sail with thin film photovoltaic cells. |
For example, the payload of a solar sail can maneuver independently. Several sailing missions propose dropping a capsule during a flyby of Mars so that it can aerobrake to the surface. This saves on having the solar sail fight the planet’s gravity all the way down to a low orbit and then back out to escape velocity. A payload could also detach and use its own thrusters to go down to a planet, then rendezvous with the sail to return to interplanetary space. This can be the case with a lander with in-situ refuelling that lands nearly empty then returns to orbit nearly empty again.
 |
| A solar sail aerocapture into Saturn. |
The large area of a solar sail also makes it very useful for aerocapture. The Modern Sail has an average mass per area of 0.022 kg/m^2. The Mars 2020 mission that landed the Perseverance rover used an aeroshell with a mass per area of about 95 kg/m^2. This means the solar sail can slow down 4320x faster in Mars’ thin atmosphere.
 |
| Aerocapture into Mars orbit with a sail. |
Or more realistically: it can brake from interplanetary velocities into a Mars orbit using the thin gases present high above Mars. The same is possible with the more advanced sails in the upper atmospheres of the gas giants. Whether the sails can survive the maneuver without being damaged is another question.
 |
| A simple hybrid sail. |
A “hybrid sail” is a more interesting design where the solar sail serves double-duty as part of another propulsion system. The obvious use case is a solar collector for a photovoltaic system. The huge reflective surfaces of a solar sail interact with large amounts of solar power but only convert a tiny fraction of it into useful kinetic energy.
The Nanofilm Sail and its 4,000,000 m^2 surface area collects 5.44 GW of sunlight near Earth. If only a tiny fraction of that power is converted into electricity and fed into an ion thruster, we would get useful thrust levels throughout the solar system. It is most useful when braking towards the outer planets like Jupiter or Saturn. In that situation, the solar sail is still handling hundreds of megawatts of power but it still takes months to slow down into a capture orbit. If the Nanofilm Sail sacrificed half of its payload to a 400 kW solar-electric propulsion system weighing 200 kg (including a 9000s Isp thruster) and had 488 kg of propellant, it would be able to provide 9 Newtons of thrust anywhere. It would be enough to slow down by 20 km/s within 34.5 days. That’s an average of 0.0067 m/s^2 or 8.3x the photon-only acceleration near Jupiter. The major benefit is that when combined with gravity assists from a moon like Io, the sail only needs to slow down to (20+17.3): 37.3 km/s. That saves a massive amount of time. The usual 343 day trip that’s been reduced to 235 days with the gravity assist is further reduced to 159 days with the electric thruster. An even greater benefit is to be had near Saturn. At that distance, the sail is still capturing 59.3 MW of power but the photon-only acceleration falls to just 0.00024 m/s^2. The electric thruster would provide 28x that much acceleration. And it would mean the sail only needs to slow down to (20+12.6):32.6 km/s, which shortens the 748 day trip to 364 days!
Similar calculations can be made for the other sails. There may be trade-offs where adding an engine and propellant to the payload lowers the sail’s characteristic acceleration but shortens the overall trip. You only need to find the right balance. This tends to favour high power density (W/kg) propulsion systems with very high specific impulse. However, do be wary of the fact that many propulsion systems cannot easily be scaled down. A Modern Sail with 1 kg of payload might find room for cold-gas micro-thrusters but probably not for an electromagnetic nozzle. The sails themselves are very fragile so an unshielded nuclear reactor is not a good idea either.
The ultimate hybrid sail is probably one where the sail material serves as a photonic thruster near the Sun, and then a second stage is used for braking for which the sail material is consumed as propellant.
 |
| A plasma thruster - VASIMR - could theoretically use aluminium gas as propellant. |
Imagine a plasma thruster that can turn solar sail material into a cloud of ions, ready to be shot out of a nozzle by magnetic fields. Apply this idea to the Diffractive Meta-Sail design. The sail alone represents 75% of the total mass of the vehicle. Its massive 2,500,000,000 m^2 area can capture 3.4 TW of sunlight near Earth, decreasing to 125.6 GW near Jupiter and 9.23 GW near Uranus. Instead of redirecting 90% of that sunlight into empty space to produce photon thrust, it could focus it instead onto an advanced photovoltaic receiver behind the sail. A 200 MW propulsion system (30% efficiency) would never need more than 666 MW of Sunlight, or 7% of the sail area to function. We can therefore consume 93% of the sail material as propellant and still have enough area to power the plasma thruster. The overall mass ratio is 3.3. The electric propulsion system would occupy half the payload capacity (5 tons) if we assume a fantastic power density of 40 kW/kg, achievable with fully superconducting designs. If the plasma thruster has a specific impulse of 12,000s, we’d get an average acceleration of 0.13 m/s^2 and a total of 140.5 km/s of deltaV.
In other words, a Diffractive Meta-Sail that swaps out half its payload for a high-Isp propulsion system could shorten its 112 day trip to Jupiter to less than 44 days. It would use its solar sail to accelerate all the way out to 2.1 AU, reaching a peak velocity of 210.8 km/s, before braking, then switching to its electric thruster for the last 12.5 days. The final maneuver is a capture around Io at 17.3 km/s.
Could we have just relied on the electric thruster alone? Probably not. The solar sail provided a ‘free’ 263.8 km/s of deltaV - more if we count the climb out of Earth’s gravity. An electric-only mission would have to provide a full (263.8+140.5): 404.3 km/s of deltaV to complete the same mission. Even with 12,000s Isp, that entails a mass ratio of 31, which is totally impractical.
 |
| The fission sail concept uses a very thin layer of uranium. Fission events are started by antimatter or neutrons from a nuclear reactor. |
There are even more options for combining propulsion systems with a solar sail. Solar thermal thrusters would provide a quick burst of thrust but not much deltaV. The backside of a solar sail could be coated with radioactive materials, turning it into a two-sided fission sail.
.jpg) |
| The electric sail rides the solar wind instead of sunlight. |
The sail could be electrically charged, turning it into an electric sail that rides the solar wind. That resource is available everywhere in the solar system and doesn't have the same drop-off as sunlight. We can imagine a craft that starts as a solar sail, then consumes its sail materials and spins them back out as a web of charged elements, creating a much larger electric sail.
Riding more than sunlight
 |
| A massive 'pinwheel' helio-gyro with human-sized payload capacity. |
In previous ToughSF posts, we frequently mention how well space infrastructure pairs with various propulsion systems. The same goes for solar sails.
A simple example would be space tugs. They would move solar sails out of the deep gravity wells of planets, saving them the weeks of spiralling outwards to deep space. Or, they could ‘catch’ sails coming in from interplanetary trajectories, which would be especially useful for settlements around Jupiter or Saturn waiting for cargo deliveries.
 |
| There is no reason why a solar sail couldn't also work as a laser sail (with low intensity beams) |
Another well-described piece of space infrastructure is beamed power. Laser beams especially work very well with solar sails. Most sails would be able to receive a large range of laser wavelengths owing to the fact that they are supposed to reflect most solar wavelengths from UV to infrared. Lasers could boost solar sails away from Earth, or help them brake into capture orbits around the gas giants. The beam energy can be used to directly provide thrust via radiation pressure, or indirectly by being directed in hybrid sails that have photovoltaic cells to power electric thrusters (and similar designs). We’ve mentioned already how reducing the braking deltaV can drastically shorten trip times.
 |
| A Skyhook is a low orbit rotating tether. |
Rotating tethers are another classic example. They can fling solar sails into higher orbits or catch them on the way down. If a solar sail is too fragile to survive the g-forces from swinging around a tether, it could detach its payload and the two would go separate ways: the payload making a short trip down a rotating tether and the sail performing long spirals to park in another orbit.
One unique pairing between tethers and sails is the ‘self-winding tether’. In this previous post, we explained how tethers are two-way momentum exchange devices. They absorb momentum from incoming payloads, store it, and then spend momentum to launch payloads to higher orbits. An imbalance between incoming and outgoing momentum has to be compensated by using rocket engines or electrodynamic propulsion. But what if there wasn’t an ambient magnetic field to exploit or enough propellant to keep up with the demand for momentum? The solution would be a solar sail. It could carry a dumb weight up to a high altitude then ‘drop it’ down to the tether. The tether absorbs its momentum. The sail then spirals down to the tether’s orbit, picks up the weight again and carries it back up for another drop. This process can be repeated indefinitely, with nothing expended except free sunlight.
Solar sails can also enable mass stream propulsion. Basically, many sails in a row, all working together like a train, carry a number of masses each. The sails head out on a long loop that takes them far away from where another spaceship is sitting. They then accelerate back in, picking up free velocity from sunlight. At the last moment, they all drop their masses and divert to the side. The masses continue in a stream up to a high velocity rendezvous with the spaceship. If the spaceship has a sort of receiver/nozzle like a pusher plate, magnetic nozzle or other such device, it can ‘ride’ the mass stream without having to spend any energy or propellant of its own. The mass stream effectively concentrates the energy gathered by solar sails over a long period into short bursts.
 |
| A fleet of solar sails, perhaps bringing a mass stream up to speed. |
Mass stream propulsion has been described in previous posts. Essentially, it strips a spaceship down to just a payload and a nozzle. The nozzle converts the mass stream into thrust. Since the spaceship does not have propellant, reactors, radiators or any such equipment, it is very lightweight. Thrust comes externally without being limited by mass ratios, and it can be used to both accelerate and brake. Combined, we get a way to accelerate hard up to incredible velocities for rapid trips around the solar system.
 |
| The high velocity masses would be consumed in a magnetic nozzle like this one. |
If sails use the SunDiver maneuver, we get sails up to 400 km/s and beyond. They would release (or become, with sacrificial micro-sails) mass streams that drift to a rendezvous with a mass-stream-rider spaceship, which would also accelerate to those velocities. It’s enough for an Earth to Saturn trip in less than 37 days. Braking would be handled by pre-positioned mass streams orbiting the destination. Best of all, the energy to drive all these mass streams is gathered for free from the Sun. There would be no need for giant railguns positioned at both the departure and destination points!
Another feature of solar sails can be exploited to maximum effect. Sails with a lightness ratio better than one can position themselves anywhere as statites. This means that rotating tethers or laser beams and relay mirrors can be placed wherever they are needed. A statite could release a string of masses at the right place to act as a slow mass stream that a fast spaceship can brake into. There’s a huge range of creative uses for equipment or mass that can be moved freely to any point in the Solar System.
Sailing prospects
So, where and how could Solar Sails be used?
We’ve clearly shown how solar sails are not necessarily slow or restricted to small payloads. They can get to places quickly and are very flexible in their uses. Solar sailing should become commonplace in the future.
Solar sails are most likely to be used to send low-cost probes to the rocky planets first. Then they would find use as ‘asteroid hoppers’ travelling from asteroid to asteroid as long their control electronics keep working. ‘Moon Tour’ missions where they survey the many bodies orbiting Jupiter and Saturn would come later. These sorts of missions make use of sails’ zero-propellant travel capability. What happens next is more speculative.
 |
| The 'Lunar Flashlight' uses the sail as large light source to explore the Moon. |
Nuclear propulsion in the future may be fast, but it costs fuels like uranium or tritium. Solar sailing is nearly free once the sail is built. There will always be a niche for ‘free’.
Sails could be used to return precious metals from asteroids back to Earth. They can redirect whole asteroids, given enough time - for either Earth's defense or other operations.
 |
| Only a 'free' propulsion system could make use of large masses of otherwise low value resources, like icy comets |
 |
| Mining with sails. |
Once we master solar sail technology and produce better lightness ratio designs, the options expand greatly. Uncrewed missions could use gigantic solar sails to carry payloads anywhere in the solar system. Passengers would use mass streams accelerated by solar sails to get to distant locations within days or weeks. Hybrid sails would bridge the gap for payloads that don’t need to get to places so quickly, or could be used when transport infrastructure is not available.
 |
| A sail on a 'non-Keplerian' orbit. |
Beamed power infrastructure to keep colonies alive around icy moons could rely on mirror relays held in position by statites. We might even see huge sail ‘motherships’ that have an onboard laser to move around a fleet of smaller dedicated laser sails. Meanwhile, statites sitting over the Sun’s poles read solar activity and warn everyone else of approaching solar storms within minutes.
The possibilities are numerous. Don’t dismiss solar sailing!








.jpg)

.jpg)















Great post, I'm so glad to see you back!
ReplyDeleteFor the 2% c interstellar sails I wonder how much they would slow down due to drag from the interstellar medium. How much velocity could you shed by unfurling the sail a few decades before you reach your destination?
Hey, thanks for sticking around.
DeleteThe interstellar medium is very thin. 1 atom per cm^3 is about 1.6x10^-21 kg/m^3. At 2% of the speed of light, the drag force is roughly 0.03 microNewtons per square meter. A sail with an Area density of 1 g/m^2 would slow down by about 1 m/s after 1 year when travelling through this medium...
A sail can be used to brake into the destination star just as effectively as it can be used to launch off the departure star.
Huh, that's quite a bit less than I expected given how much I had heard about using magnetic sails for decelerating starships, though I suppose those can be lighter and are typically considered with faster craft. That's good I guess in that the sail would not slow the craft down excessively if left unfurled so you wouldn't have to ditch or collapse it. On the other hand you might still want to collapse it if you want it in good condition to decelerate at the target star. Several centuries of 2% gas and dust impacts might not slow it much but it would probably do noticable damage to some of the thinner sail types.
DeleteMagnetic sails have been suggested from slowing down from 20% of the speed of light, which is quite a lot more than solar sails are capable of! And indeed, ultrathin materials are unlikely to survive an interstellar trip while exposed.
DeleteYou could always turn the sail sideways during the interstellar coast phase.
DeleteGood to see this post, and wow, what a lot to chew over. Thank you. Love what you do here.
ReplyDeleteThanks for the kind words.
DeleteI wonder how well it would work for extracting materials from the outer Solar System or even the Oort Cloud. It could be possible to use fission or fusion to power a laser (on the body from which one is extracting materials) accelerating both sail and payload, followed by a long inward fall towards the Sun, where the sun diving technique could be used to slingshot it out…
ReplyDeleteThe lack of sunlight would be an overwhelming obstacle to solar sails out there. But sails don't have to be universally best at everything... the outer solar system is where you go to experiment with other forms of propulsion!
DeleteGreat post, I love all the things you can do with sails. Although I wish you touched on plasma sails more here, in my view they combine the best of solar and electric sails especially when its speed that you want, you get a hyberbolic trajectory to Jupiter in 30 days - without needing to perform a Sundive maneuver first since it rides the solar wind once free of Earth's magnetosphere, so it has huge advantages there mainly near instant acceleration to interplanetary speeds. E-sails can do the same but are more limited in acceleration. One obvious caveat here is the uncertainty in plasma sail performance, so far only solar sails have been flown in space and proven the concept but same can't be said for electric or plasma sails sadly.
ReplyDeletePlasma sails, their various designs and especially the Q-drive/Windrider concept will get their own separate post, I promise!
DeleteAwesome! I can't wait honestly I want to know more about everything possible with them like this post had everything possible with solar sails including a lot of things I didn't know.
DeleteExtremely intrigued by the idea of plasma sails as a means of interstellar travel. So happy you are back!
DeleteThe concept of solar sails has come a long way since the 50s. They were considered fragile and easily destroyed with space debree.
ReplyDeletePlasma sailing deserves its own separate treatment.
DeleteThanks for sticking around!
Glad to see you back ! I wonder how useful advanced solar sails could be as weapons ?
ReplyDeleteSure, it would be useless as an anti-ship weapon, but it would be great for planetary bombardment, even for very advanced civs.
There isn't much you can do about a swarm of millions of small tungsten chunks (maybe 1g ? 100g ? 1kg ? I don't know which would be best) coming your way at 80+ km/s, and it has the massive advantage over torch missiles or other sophisticated weapons of being dirt cheap !
And now that I think about it, it could even be used as anti-ship weapons (not for any sort of rapid response of course) even if indirectly. You could use a big solar sail to accelerate a payload of thousands of small guided missiles to ludicrous speed and release them close to the parked enemy fleet for devastating effects (assuming you can overwhelm their point defense).
Thanks!
DeleteI can see a role for solar sails bombarding a small airless body where an enemy has hidden themselves inside of it, but not really any other situation. Even an ultra-high performance sail with an acceleration of 0.26 m/s^2 would take 85 hours to get up to 80 km/s. It would be bright and highly visible during that time. So any target will have to be unable to respond or escape within 85 hours...!
What solar sails could do is generate mass streams for propelling space warships to their destination quickly and cheaply.
I was more thinking about structure bombardment at extreme range for very cheap, it's not like a colony can dodge ^^ (I say that but with how filled with radiation space is, I expect underground colonies to be rather trendy on airless bodies, which would make any sort of bombardment more difficult... but that just mean we need more sails, which make the cheapness even more attractive ! )
DeleteA mass stream can become an effective digging tool. High velocity impactors are indeed being developed for getting through several meters of rock right now, on Earth. The question really is whether you can deliver these streams and dig through the regolith or armor faster than the target can devise a counter-attack or an intercept.
DeleteSolar sails are used as weapons in Alastair Reynolds' Revelation Space trilogy: a sail is released behind a ship that is being pursued, and a laser is used to decelerate it toward the pursuer. The resulting collision destroys the pursuing craft.
ReplyDeleteThat just sounds like a laser-accelerated missile!
DeleteSpeaking of which---lasers look to get more powerful
Deletehttps://phys.org/news/2023-06-photonic-crystal-surface-emitting-laser-built-bright.html
"The researchers plan to continue scaling up their laser, hoping to bring the diameter to 10mm, which would allow for producing a 1-kilowatt beam."
--publiusr
Excellent, in-depth work. Once possible trick to add to the diffraction sail- and to the Cassegrain / photon thruster: the "Forward / Starshot" trick... Apparently you don't need an actual hemispherical sail- you can achieve the same result by imprinting a-hologram-of-a-hemisphere onto a flat reflective disk.
ReplyDeleteThank you.
DeleteAre you referring to the retro-reflector idea for a solar sail that adds a 'second stage' to it, so it can brake?
Okay, I understand.
DeleteString these in a row for power beaming
ReplyDeletehttps://nautilus-array.space/
Light/MAGSAIL two-fer?
https://phys.org/news/2023-07-scientists-one-step-laser-synthesis-method.amp
Europe’s SSP plan
https://ideas.esa.int/m3#object_ac96bcaf9d2ee78fe3df65a4112539b7
Forgetamori had an article about an asteroid hitting the sun causing a plasma laser
Very late to the party, but I would be interested in a follow up article that focused on laser sails. They have been proposed for interstellar missions, though I would have to think they would be even better adapted for interplanetary ones. The addition of a laser would perhaps reduce the need for advanced materials technology for the sails.
ReplyDeleteAll photon sail work on same physical principles (150MW/N), but swapping free solar photons for laser changes equation drastically. Using kinetic stream is always going to be more efficent on interplanetary distances because ships will never realistically achieve high relativistic velocities at which stream looses it's effectivness.
DeleteLaser sails would still be better for interstellar travel: the kinetic streams would have less relative momentum, and would be knocked off course, while the laser has no such issues. However, they don't really help with simplicity: It can be lighter, but the requirement to survive up to MW/m^2 makes it probably harder anyway. Their niche is for ultra-high velocity, ultra-long distance trips like interstellar ones, where both kinetic streams and solar sails are inadequate.
DeleteGreat insights on ISO standards! For professional ISO certification services, visit BCAGL, ISO 9001, ISO 14001, and ISO 45001.
ReplyDelete