Nuclear Reactor Lasers: from Fission to Photon

Nuclear reactor lasers are devices that can generate lasers from nuclear energy with little to no intermediate conversion steps. 

We work out just how effective they can be, and how they stack up against conventional electrically-powered lasers. You might want to re-think your space warfare and power beaming after this. 

Nuclear energy and space have been intertwined since the dawn of the space age. Fission power is reliable, enduring, compact and powerful. These attributes make it ideal for spacecraft that must make every kilogram of mass as useful and as functional as possible, as any excess mass would cost several times its weight in extra propellant. They aim for equipment for the highest specific power (or power density PD), meaning that it produces the most watts per kilogram.

Lasers use a lasing medium that is rapidly energized or ‘pumped’ by a power source. Modern lasers use electric discharges from capacitors to pump gases, or a current running through diodes. The electrical power source means that they need a generator and low temperature radiators in addition to a nuclear reactor… these are significant mass penalties to a spaceship.

Fission reactions produce X-rays, neutrons and high energy ions. The idea to use them to pump a lasing medium has existed ever since the first coherent wavelengths were released from a ruby crystal in 1960. 

Much research has been done in the 80s and 90s into nuclear-pumped lasers, especially as part of the Strategic Defense Initiative. If laser power can be generated directly from a reactor, there could be significant gains in power density.

The research findings on nuclear reactor lasers were promising in many cases but did not succeed in convincing the US and Russian governments to continue their development. Why were they unsuccessful and what alternative designs could realize their promise of high power density lasers?

Distinction between NBPLs and NRLs

Most mentions of nuclear pumped lasers relate to nuclear bomb-pumped lasers. They are exemplified by project Excalibur: the idea was to use the output of a nuclear device to blast metal tubes with X-rays and have them produce coherent beams of their own. 

We will not be focusing on it.

The concept has many problems that prevent it from being a useful replacement for conventional lasers. You first need to expend a nuclear warhead, which is a terribly wasteful use of fissile material. Only a tiny fraction of the warhead’s X-rays, which are emitted in all directions, are intercepted by the metal tube. From those, a tiny fraction of its energy is converted into coherent X-rays. If you multiply both fractions, you find an exceedingly low conversion ratio. 

Further research has revealed this to be on the order of <0.00001%. It also works for just a microsecond, each shot destroys its surroundings and its effective range is limited by relatively poor divergence of the beam. These downsides are acceptable for a system meant to take down a sudden and massive wave of ICBMs at ranges of 100 to 1000 kilometers, but not much else.

Instead, we will be looking at nuclear reactor pumped lasers. These are lasers that draw power from the continuous output of a controlled fission reaction.

Performance

We talk about efficiency and power density to compare the lasers mentioned in this post. How are we working them out?

For efficiency, we multiply the reactor’s output by the individual efficiencies of the laser conversion steps, and assume all inefficiencies become waste heat. The waste heat is handled by flat double-sided radiator panels operating at the lowest temperature of all the components, which is usually the laser itself.

This will give a slightly poorer performance than what could be obtained from a real world engineered concept. The choice of radiator is influenced by the need for easy comparison instead of maximizing performance in individual designs.

We will note the individual efficiencies as Er for the reactor, El for the laser and Ex for other components. The overall efficiency will be OE.

• OE = Er * Ex * El * Eh

In most cases, Er and Eh can be approximated as equal to 1. As we are considering lasers for use in space with output on the order of several megawatts and beyond, it is more accurate to use the slope efficiency of a design rather than the reported efficiency. Laboratory tests on the milliwatt scale are dominated by the threshold pumping power, which cuts into output and reduces the efficiency. As the power is scaled up, the threshold power becomes a smaller and smaller fraction of the total power.

Calculating power density (PD) in Watts per kg for several components working with each other’s outputs is a bit more complicated. As above, we’ll note them PDr, PDl, PDh, PDx and so on. The equation is:

• PD = (PDr * OE) / (1 + PDr (Ex/PDx + Ex*El/PDl + (1 - Ex*El)/PDh))

Generally, the reactor is a negligible contributor to the total mass of equipment, as it is in the several hundred kW/kg, so we can simplify the equation to:

• PD = OE / (Ex/PDx + Ex*El/PDl + (1 - Ex*El)/PDh)

Inputting PDx, PDl and PDh values in kW/kg creates a PD value also in kW/kg.

Direct Pumping

The most straightforward way of creating a nuclear reactor laser is to have fission products interact directly with a lasing medium. Only gaseous lasing mediums, such as xenon or neon, could survive the conditions inside a nuclear reactor indefinitely, but this has not stopped attempts at pumping a solid lasing medium.

Three methods of energizing or pumping a laser medium have been successful.

Wall pumping

Wall pumping uses a channel through which a gaseous lasing medium flows while surrounded by nuclear fuel. The fuel is bombarded by neutrons from a nearby reactor. The walls then release fission fragments that collide with atoms in the lasing medium and transfer their energy to be released as photons. The fragments are large and slow so they don’t travel far into a gas and tend to concentrate their energy near the walls. If the channels are too wide, the center of the channel is untouched and the lasing medium is unevenly pumped. This can create a laser of very poor quality.

To counter this, the channels are made as narrow as possible, giving the fragments less distance to travel. However, this multiplies the numbers of channels needed to produce a certain amount of power, and with it the mass penalty from having many walls filled with dense fissile fuel.

The walls absorb half of the fission fragments they create immediately. They release the surviving fragments from both faces of fissile fuel wall. So, a large fraction of the fission fragment power is wasted. They are also limited by the melting temperatures of the fuel. If too many fission fragments are absorbed, the heat would the walls to fail, so active cooling is needed for high power output.

The FALCON experiments achieved an efficiency of 2.5% when using xenon to produce a 1733 nm wavelength beam. 

Gas laser experiments at relatively low temperatures reported single-wavelength efficiencies as high as 3.6%. The best reported performance was 5.6% efficiency from an Argon-Xenon mix producing 1733 nm laser light, from Sandia National Laboratory. 

Producing shorter wavelengths using other lasing mediums, such as metal vapours, resulted in much worse performance (<0.01% efficiency).

Higher efficiencies could be gained from a carbon monoxide or carbon dioxide lasing medium, with up to 70% possible, but their wavelengths are 5 and 10 micrometers respectively (which makes for a very short ranged laser) and a real efficiency of only 0.5% has been demonstrated.

One estimate presented in this paper is a wall-pumped mix of Helium and Xenon that converts 400 MW of nuclear power into 1 MW of laser power with a 1733 nm wavelength. It is expected to mass 100 tons. That is an efficiency of 0.25% and a power density of just 10 W/kg.

It illustrates the fact that designs meant to sit on the ground are not useful references.

A chart from this NASA report reads as a direct pumped nuclear reactor laser with 10% overall efficiency having a power density of about 500 W/kg, brought down to 200 W/kg when including radiators, shielding and other components.

Volumetric pumping

Volumetric pumping has Helium-3 mixed in with a gaseous lasing medium to absorb neutrons from a reactor. 

Neutrons are quite penetrating and can traverse large volumes of gas, while Helium 3 is very good at absorbing neutrons. When Helium-3 absorbs neutrons, it creates charged particles that in turn energize lasing atoms when they enter into contact with each other. Therefore, neutrons can fully energize the entire volume of gas. The main advantages of this type of laser pumping is the much reduced temperature restrictions and the lighter structures needed to handle the gas when compared to multiple narrow channels filled with dense fuel.

However, Helium-3 converts neutrons into charged particles with very low efficiency, with volumetric pumping experiments reporting 0.1 to 1% efficiency overall. This is because the charged particles being created contain only a small portion of the energy the Helium-3 initially receives.

Semiconductor pumping

The final successful pumping method is direct pumping of a semiconductor laser with fission fragments. The efficiency is respectable at 20%, and the compact laser allows for significant mass savings, but the lasing medium is quickly destroyed by the intense radiation. It consists of a thin layer of highly enriched uranium sitting on a silicon or gallium semiconductor, with diamond serving as both moderator and heatsink.

There are very few details available on this type of pumping. 

A space-optimized semiconductor design from this paper that suggests that an overall power density of 5 kW/kg is possible. It notes later on that even 18 kW/kg is achievable. It is unknown how the radiation degradation issue could be solved and whether this includes waste heat management equipment. Without an operating temperature and a detailed breakdown of the component masses assumed, we cannot work it out on our own.

Other direct pumped designs

Wall or volumetric pumping designs were conceived when nuclear technology was still new and fission fuel had to stay in dense and solid masses to achieve criticality. More modern advances allow for more effective forms for the fuel to take.The lasing medium could be made to interact directly with a self-sustaining reactor core. This involves mixing the lasing medium with uranium fluoride gas, uranium aerosols, uranium vapour at very high temperatures or uranium micro-particles at low temperatures.

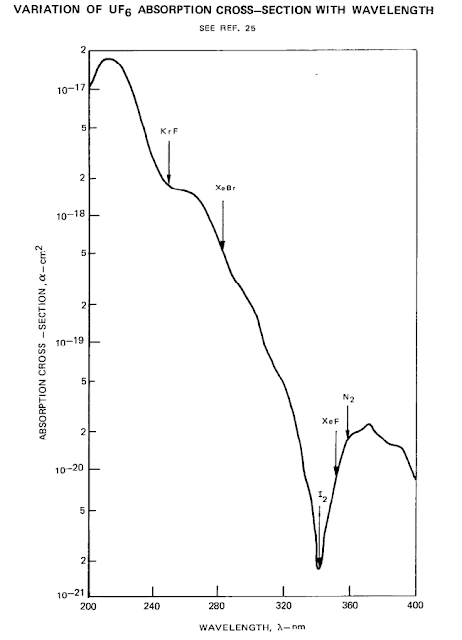
The trouble with uranium fluoride gas and aerosols or micro-particles is the tendency for them to re-absorb the energy (quenching) of excited lasing atoms. This has prevented any lasing action from being realized in all experiments so far. As this diagram shows, uranium fluoride gas absorbs most wavelengths very well, further reducing laser output.

If there is a lasing medium that is not quenched by uranium fluoride, then there is potential for extraordinary performance.

An early NASA report on an uranium fluoride reactor lasers for space gives a best figure of 73.3 W/kg from what is understood to be a 100 MW reactor converting 5% of its output into 340 nanometer wavelength laser light. With the radiators in the report, this falls to 56.8 W/kg.

If we bump up the operating temperature to 1000K, reduce the moderator to the 20cm minimum, replace the pressure vessel with ceramics and use more modern carbon fiber radiators, we can expect the power density of that design to increase to 136 W/kg.

Uranium vapours are another option. They require temperatures of 4000K and upwards but if the problem of handling those temperatures is solved (perhaps by using actively cooled graphite containers), then 80% of the nuclear output can be used to excite the lasing medium, for an overall efficiency that is increased four-fold over wall pumping designs.

More speculative is encasing uranium inside a C60 Buckminsterfullerene sphere. Fission fragments could exit the sphere while also preventing the quenching of the lasing material. This would allow for excellent transmission of nuclear power into the lasing medium, without extreme temperature requirements.  

Nuclear-electric comparison

With these numbers in mind, it does not look like direct pumping is the revolutionary upgrade over electric lasers that was predicted in the 60s.

Turbines, generators, radiators and laser diodes have improved by a lot, and they deliver a large fraction of a reactor’s output in laser light. We expect a space-optimized nuclear-electric powerplant with a diode laser to have rather good performance when using cutting edge technology available today.

With a 100 kW/kg reactor core, a 50% efficient turbine at 10 kW/kg, an 80% efficient electrical generator at 5 kW/kg, powering 60% efficient diodes at 7 kW/kg and using 1.34 kW/kg radiators to get rid of waste heat (323K temperature), we get an overall efficiency of 24% and a power density of 323 W/kg.

A more advanced system using a very powerful 1 MW/kg reactor core, a 60% efficient MHD generator at 100 kW/kg with 1000K 56.7 kW/kg radiators, powering a 50% efficient fiber laser cooled by 450K 2.3 kW/kg radiators, would get an overall efficiency of 30% and a power density of 2.5 kW/kg. 

Can we beat these figures with reactor lasers?

Indirect pumping

The direct pumping method uses the small fraction of a reactor’s output that is released in the form of neutrons, or problematic fission fragments. Would it not be better to use the entire output of the nuclear reaction?

Indirect pumping allows us to use 100% of the output in the form of heat. This heat can then be converted into laser light in various ways.

Research and data for some of the following types of lasers comes from solar-heated designs that attempt to use concentrated sunlight to heat up an intermediate blackbody that in turn radiates onto a lasing medium. For our purposes, we are replacing the heat of the Sun with a reactor power source. It is sometimes called a ‘blackbody laser’ in that case.

Blackbody radiation pump

At high temperatures, a blackbody emitter radiates strongly in certain wavelengths that lasing materials can be pumped with. A reactor can easily heat up a black carbon surface to temperatures of 2000 to 3000K – this is what nuclear rockets are expected to operate at anyhow.

Some of the spectrum of a blackbody at those temperatures lies within the wavelengths that are absorbed well by certain crystal and gaseous lasing mediums.

Neodymium-doped Ytrrium-Aluminium-Garnet (Nd:YAG) specifically is a crystal lasing medium that has been thoroughly investigated as a candidate for a blackbody-pumped laser. It produces 1060 nm beams.

Efficiency figures vary.

A simple single-pass configuration results in very poor efficiency (0.1 to 2%). This is because the lasing medium only absorbs a small portion of the entire blackbody spectrum. In simpler terms, if we shine everything from 100 nm to 10,000 nm onto a lasing medium, it will convert 0.1 to 2% of that light into a laser beam and turn the rest into waste heat. With this performance, blackbody pumped lasers are no better than direct pumped reactor laser designs from the previous section.

Instead, researchers have come up with a way to recover the 99 to 99.9% of the blackbody spectrum that the lasing medium does not use. This is the recycled-heat blackbody pumped laser.

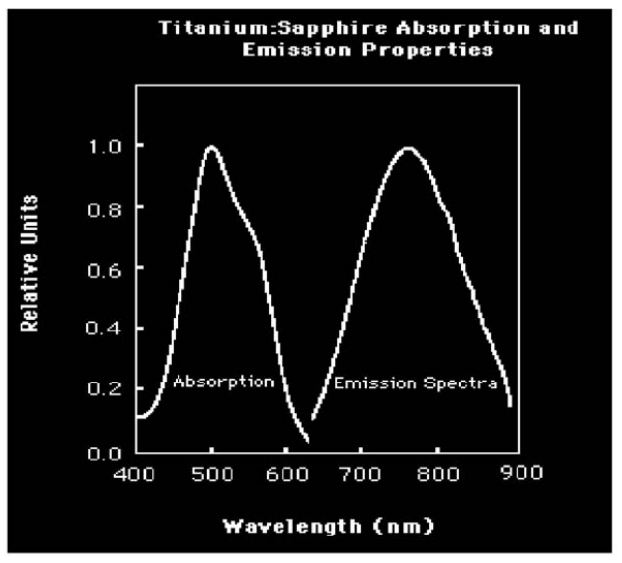
An Nd:YAG crystal sits inside a ‘hot tube’. Blackbody radiation coming from the tube walls passes through the crystal. The crystal is thin and nearly transparent to all wavelengths. The illustration above uses Ti:Sapphire but the concept is the same for any laser crystal.

Only about 2% of blackbody spectrum is absorbed with every pass through the crystal. The remaining 97 to 98% pass through to return to the hot tube’s walls. They are absorbed by a black carbon surface and recycled into heat. Over many radiation, absorption and recycling cycles, the fraction of total energy that becomes laser light increases for an excellent overall efficiency.

35% efficiency with a Nd:YAG laser was achieved.

The only downside is that the Nd:YAG crystal needs intense radiation within it to start producing a beam. The previous document suggests that 150 MW/m^3 is needed. Another source indicates 800 MW/m^3. We also know that efficiency increases with intensity. If we aim for 1 GW/m^3, which corresponds to 268 Watts shining on each square centimetre of a 1 cm diameter lasing rod, we would need a 1:1 ratio of emitting to receiving area if the emitter has a temperature of at least 2622K. 

From a power conversion perspective, a 98% transparent crystal that converts 35% of spectrum it absorbs means it is only converting 0.7% of every Watt of blackbody radiation that shines through it. So, a crystal rod that receives 268 Watts on each square centimetre will release 1.87 W of laser light.

We can use the 1:1 ratio of emitter and receiver area to reduce weight and increase power density. Ideally, we can stack emitter and receiver as flat surfaces separated by just enough space to prevent heat transfer through conduction.

Reactor coolant channels, carbon emitting surface (1cm), filler gas, Nd:YAG crystal (1cm) and helium channels can be placed back to back. The volume could end up looking like a rectangular cuboid, interspaced by mirror cavities.

20 kg/m^2 carbon layers and 45.5 kg/m^2 crystal layers that release 1.87 W per square centimetre, with a 15% weight surplus for other structures and coolant pipes, puts this component’s power density at about 250 W/kg.

The laser crystal is cooled from 417K according to the set-up in this paper. Getting rid of megawatts at such a low temperature is troublesome. Huge radiator surface areas will be required.

As we are using flat panel radiators throughout this post, we have only two variables: material density, material thickness and operating temperature. The latter is set by the referenced document.

We will choose a 1mm thick radiator made of low density polyethylene. We obtain 0.46 kg/m^2 are plausible. When radiating at 417K, they could achieve 3.73 kW/kg.

It is likely that they will operate at a slightly lower temperature to allow for a thermal gradient that transfers heat out of the lasing medium and into the panels, and the mass of piping and pumps is not to be ignored, but it is all very hard to estimate and is more easily included in a 15% overall power density penalty for unaccounted-for components.

A 100 kW/kg reactor, 250 W/kg emitter-laser stack and 3.73 kW/kg radiators would mean an overall power density of 188 W/kg, after applying the penalty.

Gaseous lasing mediums could hold many advantages over a crystal lasing medium. They require much less radiation intensity (W/m^3) to start producing a laser beam. This research states that an iodine laser requires 450 times less intensity than an equivalent solid-state laser. It is also easier to cool a gas laser, as we can simply get the gas to flow through a radiator. On the other hand, turbulent flow and thermal lensing effects can deteriorate the quality of a beam into uselessness.

No attempts have been reported on applying the heat recycling method from the Nd:YAG laser to greatly boost efficiency in a gas laser. Much research has been performed instead on direct solar-pumped lasers where the sunlight passes through a gaseous medium just once.

The Sun can be considered to be a blackbody emitter at a temperature of 5850K. Scientists have found the lasing mediums best suited to being pumped by concentrated sunlight – they absorb the largest fraction of the sunlight’s energy.

That fraction is low in absolute terms, meaning poor overall performance. An iodine-based lasing medium reported 0.2% efficiency. Even worse efficiency of 0.01% was achieved when using an optically-pumped bromine laser. Similarly, C3F7I, an iodine molecule which produces 1315 nm laser light, was considered the best at 1% efficiency.

Solid blackbody emitters are limited to temperatures just above 3000K. There would be a great mismatch between the spectrum this sort of blackbody releases and the wavelengths the gaseous lasing mediums cited above require. In short, the efficiency would fall below 0.1% in all cases.

One final option is Gallium-Arsenic-Phosphorus Vertical External Cavity Surface Emitting Laser (VECSEL) designed for use in solar-powered designs. It can absorb wavelengths between 300 and 900nm, which represents 65% of the solar wavelengths but only 20% of the radiation from a 3000K blackbody. This works out to an emitter with a power density of 45.9 kW/kg. 

The average efficiency is 50% when producing a 1100nm beam. Since it is extracting 20% of the wavelengths from the emitter, this amounts to 10% overall efficiency.

Using the numbers in this paper, we can surmise that the VECSEL can handle just under 20 MW/kg. The mass of the laser is therefore negligible. With a 100 kW/kg reactor, we work out a power density of 3.1 kW/kg.

VECSELs can operate at high temperatures, but they suffer from a significant efficiency loss. We will keep them at 300K at most. It is very troublesome as 20 MW of light is needed to be concentrated on the VECSEL to start producing a laser beam. 90% of that light is being turned into waste heat within a surface a few micrometers thick. Diamond heatsink helps in the short term but not in continuous operation.

Radiator power density will suffer. Even lightweight plastic panels at 300K struggle to reach 1 kW/kg. When paired with the previous equipment and under a 15% penalty for unaccounted for components, it means an overall power density of 91 W/kg.

This illustrates why an opaque pumping medium is unsuitable for direct pumping as it does not allow for recycling of the waste heat.

Filtered blackbody pumping

A high temperature emitter radiates all of its wavelengths into the blackbody-pumped lasing medium. We described a method above for preventing the lasing medium from absorbing 98 to 99.9% of the incoming energy and turning it immediately into waste heat. The requirement was that the lasing medium be very transparent to simply let through the unwanted wavelengths.

However, this imposes several design restrictions on the lasing medium. It has to be thin, it has to be cooled by transparent fluids, and it might have to sit right next to a source of high temperature heat while staying at a low temperature itself.

We can instead filter out solely the laser pumping wavelengths from the blackbody spectrum and send those to the lasing medium while recycling the rest. 

The tool to do this is a diffraction grating. There are many other ways of extracting specific wavelengths from a blackbody radiation spectrum, such as luminescent dyes or simple filters, but this method is the most efficient.

Like a prism, a diffraction grating can separate out wavelengths from white light and send them off in different directions. For most of those paths, we can put a mirror in the way that send the unwanted wavelengths back into the blackbody emitter. For a small number of them, we have a different mirror that reflects a specific wavelength into the lasing medium.

A lasing medium that receives just a small selection of optimal wavelengths is called optically pumped. It is a common feature of a large number of lasers, most notably LED-pumped designs. We can use them as a reference for the potential performance of this method.

We must note that while we can get high efficiencies, power is still limited, as in the previous section. Extracting a portion of the broadband spectrum that the lasing medium accepts also means that power output is reduced to that portion.

Another limitation is the temperature of the material serving as a blackbody emitter. The nuclear reactor that supplies the heat to the emitter is limited to 3000K in most cases, so the emitter must be at that temperature or lower (even if a carbon emitter can handle 3915K at low pressures and up to 4800K at high pressures, while sublimating rapidly).

Thankfully, the emission spectrum of a 3000K blackbody overlaps well with the range of wavelengths an infrared fiber laser can be pumped with.

A good example is an erbium-doped lithium-lanthanide-fluoride lasing medium in fiber lasers. We could use it to produce green light as pictured above, but invisible infrared is more effective. 

As we can see from here, erbium absorbs wavelengths between 960 and 1000 nm rather well. It re-emits them at 1530 nm wavelength laser light with an efficiency reported to be 42% in the ‘high Al content’ configuration, which is close the 50% slope efficiency.

In fact, the 960-1000 nm band represents 2.7% of the total energy emitted. It is absorbing 125 kW from each square meter of emitter. If the emitter is 1 cm thick plate of carbon and the diffraction grating, with other internal optics needed to guide light into the narrow fiber laser, are 90% efficient, then we can expect an emitter power density of about 5.6 kW/kg.

Another example absorbs 1460 to 1530 nm light to produce a 1650 nm beam. This is 3.7% of the 3000K emitter’s spectrum, meaning an emitter power density of 7.7 kW/kg. 

The best numbers come from ytterbium fiber lasers. They have a wider band of wavelengths that can be pumped with, 850 to 1000 nm (which is 10.1% of the emitter’s output), and they convert it into 1060 nm laser light with a very high efficiency (90%). It would give the emitter an effective power density of 23.4 kW/kg. More importantly, we have examples operating at 773K.

The respected Thorlabs manufacturer gives information about the fiber lasers themselves. They can handle 2.5 GW/m^2 continuously, up to 10GW/m^2 before destruction. Their largest LMA-20 core seems to be able to handle 38 kW/kg of pumping power. It is far from the limit. 

Based on numbers provided by this experiment, we estimate the fiber laser alone to be on the order of 95kW/kg. Another source works out a thermal-load-limited fiber laser with 84% efficiency to have a power density of 695 kW/kg before the polymer cladding melts at 473K.

We can try to estimate the overall power density of a fiber laser.

A 100 kW/kg reactor is used to heat a 23.4 kW/kg emitter, where a diffraction grating filters out 90% of the output to be fed into a fiber laser with 90% efficiency and negligible mass. The waste heat is handled by 1mm thick carbon fiber panels operating at 773K for a power density of 20.2 kW/kg.

Altogether, this gives us 11 kW/kg after we include the same penalty as before.

 

If it is too difficult to direct light from a blackbody emitter into the narrow cores of fiber lasers, then a simple lasing crystal could be used. This is unlikely, as it has already been done, even in high radiation environments.

 

Nd:YAG, liberated from the constraint of having to be nearly entirely transparent, can achieve good performance. It can sustain a temperature of 789K.

We know that Nd:YAG can achieve excellent efficiency when being pumped by very intense 808nm light to produce a 1064nm beam, of 62%. It is hoped that this efficiency is maintained across the lasing crystal’s 730 to 830nm absorption band.

A 3000K blackbody emitter releases 6% of its energy in that band. At 20 kg/m^2, this gives a power density of 13.8 kW/kg. We will cut off 10% due to losses involved in the filtering and internal optics.

As before, the laser crystal itself handles enough pumping power on its own to have a negligible mass.

The radiators operating at 789K will require carbon fiber panels. They’ll manage a power density of 22 kW/kg.

Optimistically, we can expect a power density of 3.7 kW/kg (reduced by 15%) when we include all the components necessary.

Ultra-high-temperature blackbody pumped laser

We must increase the temperature of the blackbody emitter. It can radiate more energy across the entire spectrum, and concentrates it in a narrower selection of shorter wavelengths.

Solid blackbody surfaces are insufficient. To go beyond temperatures of 4000K, we must consider liquid, gaseous and even plasma blackbody emitters. This requires us to abandon conventional solid-fuel reactors and look at more extreme designs.

There is a synergy to be gained though. The nuclear fuel can also act as blackbody emitter if light is allowed to escape the reactor.

Let us consider two very high to ultra-high temperature reactor designs that can do that: a 4200K liquid uranium core with a gas-layer-protected transparent quartz window and a 19,000K gaseous uranium-fluoride ‘lightbulb’ reactor.

For each design, we will try to find an appropriate laser that makes the best use of the blackbody spectrum that is available.

4200K:

Uranium melts at 1450K and boils at 4500K. It can therefore be held as a dense liquid at 4200K. We base ourselves on this liquid-core nuclear thermal rocket, where a layer of fissile fuel is held against the walls of a drum by centrifugal effects. The walls are 10% reflective and 90% transparent.

The reflective sections hold neutron moderators to maintain criticality. This will be beryllium protected by a protected silver mirror. It absorbs wavelengths shorter than 250 nm and reflects longer wavelengths with 98% reflectivity.

We expect the neutron moderator in the reflective sections, combined with a very highly enriched uranium fuel, to still manage criticality. The spinning liquid should spread the heat evenly and create a somewhat uniform 4200K surface acting as a blackbody emitter.   

The transparent sections are multi-layered fused quartz. It is very transparent to the wavelengths a 4200K blackbody emitter radiates – this means it does not heat up much by absorbing the light passing through.

We cannot have the molten uranium touch the drum walls. We need a low thermal conductivity gas layer to separate the fuel from the walls and act like a cushion of air for the spinning fuel to sit on. Neon is perfect for this. It is mentioned as ideal for being placed between quartz walls and fission fuel in nuclear lightbulb reactor designs. The density difference between hot neon gas and uranium fuel is great enough to prevent mixing, and the low thermal conductivity (coupled with high gas velocity) reduces heat transfer through conduction. We might aim to have neon enter the core at 1000K and exit at 2000K.

There is still some transfer of energy between the fuel and the walls because the mirrors are not perfect; about 1.8% of the reactor’s emitted light is absorbed as heat in the walls. Another 0.7% in the form of neutrons and gamma rays enters the moderator. We therefore require an active cooling solution to channel coolant through the beryllium and between the quartz layers. Helium can be used. It has the one of the highest heat capacities of all simple gases, is inert and is even more transparent than quartz. 

Beryllium and silver can survive 1000K temperatures, so that will set our helium gas temperature limit.

A heat exchanger can transfer the heat the neon picks up to the cooler helium loop. The helium is first expanded through a turbine. It radiates its accumulated heat at 1000K. It is then compressed by a shaft driven by the turbine.

If we assume that the reactor has power density levels similar to this liquid core rocket (1 MW/kg) and that 2.5% of its output becomes waste heat, then it can act as a blackbody emitter with a power density of 980 kW/kg. Getting rid of the waste heat requires 1 mm thick carbon fiber radiators operating at 1400K. Adding in the weight of those radiators and we get 676 kW/kg.

A good fit might be a titanium-sapphire laser. It would absorb the large range of wavelengths between 400 and 650 nm. 

That’s 18.5% of a 4200K emitter’s spectrum. If we use a diffraction grating to filter out just those wavelengths, and include some losses due to internal optics, we get 125 kW of useful wavelengths per kg of reactor-emitter.

The crystal can operate at up to 450K temperature, with 40% efficiency. Other experiments into the temperature sensitivity of the Ti:Al2O3 crystal reveals lasing action even at 500K, with mention of a 10% reduction to efficiency. We will use the 36% figure for the laser to be on the safe side. Based on data from this flashpumping experiment and this crystal database, we know that it can easily handle 1.88 MW/kg. The mass contribution of the laser itself is negligible.

Any wavelengths that get absorbed but are not turned into laser light become waste heat. At 450K temperature, we can still use the lower density by HDPE plastic panels to get a waste heat management solution with 4.6 kW/kg.

Putting all the components together and applying a 15% penalty just to be conservative, we obtain an overall power density of 2.2 kW/kg.

19,000:

If we want to go hotter, we have to go for fissioning gases. Gas-core ‘lightbulb’ nuclear reactors will be our model.

The closed-cycle ‘lightbulb’ design has uranium heat up to the point where it is a very high temperature gas. That gas radiated most of its energy in the form of ultraviolet light. A rocket engine, as described in the ‘NASA reference’ designs, would have the ultraviolet be absorbed by small tungsten particles seeded within a hydrogen propellant flow. 4600 MW of power was released from an 8333K gas held by quartz tubes, with a total engine mass of 32 tons.

We want to use the uranium gas as a light source. More specifically, we want to maximize the amount of energy released in wavelengths between 120 and 190 nm. 19,000K is required. It is within reach, as is shown here.

Unlike a rocket engine, we cannot have a hydrogen propellant absorb waste heat and release it through a nozzle. The NASA reference was designed around reducing waste heat to remove the need for radiators, but we will need them. Compared to the reference design, we would have 27 times the output due to the higher temperatures, but then we have to add the mass of the extra radiators. 

About 15% of the reactor’s output is lost as waste heat in the original design. It was expected that all the remaining output is absorbed by the propellant. We will be having a lasing gas instead of propellant in between the quartz tube and the reactor walls. The gas is too thin to absorb all the radiation, so to prevent it all from being absorbed by the gas walls, we will use mirrors.

Polished, UV-grade aluminium can handle the UV radiation. It reflects it back through the laser medium and into the quartz tubes to be recycled into heat. Just like the blackbody-pumped Nd:YAG laser, we can create a situation where the pumping light makes multiple passes through the lasing medium until the maximum fraction is absorbed.

Based on this calculator and this UV enhanced coating, we can say that >95% of the wavelengths emitted by a 19,000K blackbody surface are reflected.

In total, 20% of the reactor’s output becomes waste heat.

Since aluminium melts at 933K, we will keep a safe temperature margin and operate at 800K. This should have only a marginal effect on the mirror’s reflective properties. Waste heat must be removed at this temperature. As in the liquid fuel reactor, the coolant fluid passes through a turbine, into a radiator and is compressed on its way back into the reactor. Neon is used for the quartz tube, helium for the reactor walls and the gaseous lasing medium is its own coolant.

Based on the reference design, the reactor would have 4.56 MW/kg in output, or 3.65 MW/kg after inefficiencies. If the radiators operate at 750K and use carbon fiber fins, we can expect a power density for the reactor-emitter of 70.57 kW/kg.

28.9% of the radiation emitted by a 19,000K blackbody surface, specifically wavelengths between 120 and 190nm, is absorbed by a Xenon-Fluoride gas laser. 

They are converted into a 350nm beam with 10% efficiency in a single-pass experiment. In our case, the lasing medium is optically thin. Much of the radiated energy passes through un-absorbed. The mirrors on the walls recycles those wavelengths for multiple passes, similar to the Nd:YAG design mentioned previously. Efficiency could rise as high as the maximal 43%. This paper suggests the maximal efficiency for converting between absorbed and emitted light is 39%. We’ll use an in-between figure of 30%. This means that the effective power density of the reactor-emitter-laser system is 6.12 kW/kg.

The XeF lasing medium is mostly unaffected by temperatures of 800K, so long as the proper density is maintained. We can therefore cool down the lasing medium with same radiators as for the reactor-emitter (17.94 kW/kg). When we include the waste heat of the laser, we get an overall power density of 2.9 kW/kg, after applying a 15% penalty.

A better power density can be obtained by having a separate radiator for each component that absorbs waste heat (quartz tubes, lasing medium, reactor walls) so that they operate at higher temperatures, but that would be much more complex.

Aerosol fluorescer reactor

The design can be found with all its details in this paper.

Tiny micrometer-sized particles of fissile fuel are surrounded in moderator and held at high temperatures. Their nuclear output, in the form of fission fragments, escapes the micro-particles and strikes Xenon-Fluoride or Iodine gas mixtures to create XeF* or I2* excimers. These return to their stable state by releasing photons of a specific wavelength through fluorescence. Their efficiency according to the following table is 19-50%.

Simply, it is an excimer laser that is pumped by fission fragments instead of electron beams. I2* is preferred for its greater efficiency and ability to produce 342 nm beams. Technically, this is an indirect pumping method, but it shares most of its attributes with direct pumping reactor lasers.

The overall design is conservatively estimated at 15 tons overall mass, but with improvements to the micro-particle composition (such as using plutonium or a reflective coating), it could be reduced even further. It is able to produce 1 MJ pulses of 1 millisecond duration. With one pulse a second, this a power density of 66 W/kg. One hundred pulses mean 6.6 kW/kg. One thousand pulses, or quasi-continuous operation, would yield 66 kW per kg. 

The only limit to the reactor-laser’s power density is heat build-up. At 5% efficiency, there is nineteen times more waste heat than laser power leaving the reactor. We expect that using the UV mirrors from the previous design could drastically improve this figure by recycling light that was not absorbed by the lasing medium in the first pass through. Thankfully, the 1000K temperature allows for some pretty effective management of waste heat.

Carbon fiber panels of 1mm thickness, operating at 1000K would handle 56.7 kW/kg. It would give the reactor a maximum power density of 2.4 kW/kg, including a 15% penalty for other equipment.

If the reactor can operate closer to the melting point of its beryllium moderator, perhaps 1400K, then it can increase its power density to 8.3 kW/kg.

Conclusion

Reactor lasers, when designed appropriately, allow for high powered lasers from lightweight devices. We have multiple examples of designs, either from references or calculated, that output several kW of laser power per kg.

The primary limitations of many of the designs can be adjusted in ways that drastically improve performance. The assumptions made (for instance, 1 cm thick carbon emitter or flat panel radiators) are solely for the sake of easy comparison. It is entirely acceptable to use 1mm thick emitting surfaces or one of the alternate heat radiator designs mentioned in this previous blog post. Even better, many of the lower temperature lasers can have their waste heat raised to a higher temperature using a heat pump. Smaller and lighter radiators can then be used for a small penalty in overall efficiency to power the heat pumps.

Most of the lasers discussed have rather long wavelengths. This is not great for use in space, as the distances the beam has to traverse are huge and it multiplies the size of the focusing optics required. For this reason, a method of shortening the wavelengths, perhaps using frequency doubling, is recommended. Halving the wavelength doubles the effective range. However, there is a 20-30% efficiency penalty for using frequency doubling. Conversely, lasers which produce short wavelength beams have a great advantage.

The list of laser options for each type of pumping is also by no means exhaustive. There might be options not considered here that would allow for much greater performance… but research on such options is very limited. For example, blackbody and LED pumping seems to be a ‘dead’ field of research, now that diodes can produce a single wavelength of the desired power. Up-to-date performance of those options is therefore non-existent and so we cannot fairly compare their performance to lasers which have been developed in their stead.

It should be pointed out that a direct comparison between reactor and electric lasers is not the whole story. Reactor lasers can easily be converted into dual-mode use, where 100% of their heat is used for propulsion purposes. A spaceship with an electric laser can only a fraction of their output in an electric rocket. For example, the 4200K laser can have a performance close to the liquid-core rocket design it was derived from. Other, like the aerosol fluorescer laser, can both create a beam and heat propellant at the same time. A nuclear-electric system must choose where to send its electrical output and must accept the 60% reduction in overall power due to the conversion steps between heat and electricity at all times.

Finally, certain reactor lasers have hidden strength when facing hostile forces.

Mirrors work both ways. The same optics and mirrors that transport your laser beam from the lasing medium out into space and to an enemy target can be exploited by an enemy to get their beam to travel down the optics and mirrors and reach your lasing medium.

The lasing medium, assumed to be diodes or other semiconductor lasers, has to operate at relatively low temperatures and so it will melt and be destroyed under the focused glare of the enemy beam.

Tactics around using lasers and counter-lasers, something called ‘eyeball-frying contests’ can sometimes lead to a large and powerful warship being brought to a stalemate by a small counter-laser.

A nuclear reactor laser’s lasing medium can be hot gas or fissioning fuel. They are pretty much immune to the extra heat from an enemy beam. It would render them much more resistant to ‘eye-frying’ tactics. 

This, and many other strengths and consequences, become available to you if you include nuclear reactor lasers in your science fiction.

PS: I must apologize for using many sources that can only be fully accessed through a paywall. It was a necessity when researching this topic, on which little detail is available to the public. For this same reason, illustrations had to be derived from documents I cannot directly link to, but they are all referenced in links in this post.